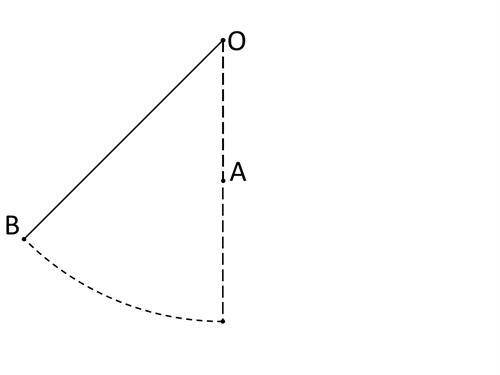
Математический маятник длиной 80 см совершает колебания параллельно вертикальной стенке. Ниже подвеса на расстоянии 40 см от точки подвеса (в точке А) в стенку забит тонкий гвоздь (смотри рисунок). Определи период колебаний такого маятника. При расчётах прими π=3,14, g=9,8 м/с². (ответ округли до сотых.)
Другие вопросы по теме Физика
Популярные вопросы
- Решите если можете! выражение: а) (x^2-10x+24/x^2-2x-24)^3 / (4x-x^2/5x+20)^3...
3 - Вгазете 7 страниц, а в журнале в 8 раз больше. сколько страниц в...
2 - Составит план на тему первые земледельцы...
3 - Король послал к шалтаю -болтаю всю королевскую конницу и всю королевскую...
3 - Округлите числа 68.823, 238.480, 2.560.511 до разряда тысяч...
3 - 7класс макарычев сколько будет 2.5+5.6×258-41...
3 - Найди сумму: 1)4 дм 6 см + 5 дм 8 см 2)8м 5 см + 6 м 96 см 3)12...
2 - Втрапеции авсд боковые стороны ав=13см сд= 15 см. периметр равен...
2 - Начертите прямую a и отметьте точку m не лежащую на ней с чёртёжного...
1 - Найдите значение выражения б) а-(б+12),если а=80,б=58...
1
Период колебаний математического маятника можно найти, используя формулу для периода колебаний физического маятника:
T = 2 * π * √(L / g),
где T - период колебаний, L - длина маятника, g - ускорение свободного падения.
В данном случае у нас есть длина маятника L = 80 см = 0,8 м и ускорение свободного падения g = 9,8 м/с².
Также из рисунка видно, что гвоздь забит на расстоянии 40 см от точки подвеса. Это означает, что точка А является новой точкой подвеса.
Теперь нужно найти новую длину маятника. Обозначим ее как L'.
L' = L - AB,
где AB - расстояние от точки подвеса до гвоздя.
В нашем случае AB = 40 см = 0,4 м.
L' = 0,8 м - 0,4 м = 0,4 м.
Теперь, подставив найденное значение новой длины маятника в формулу для периода колебаний, получим:
T = 2 * π * √(0,4 / 9,8).
Вычислим значение в скобках:
0,4 / 9,8 ≈ 0,0408.
Теперь найдем квадратный корень из этого значения:
√(0,0408) ≈ 0,202.
Подставим полученное значение в формулу для периода:
T = 2 * π * 0,202 ≈ 1,271.
Таким образом, период колебаний такого маятника примерно равен 1,271 секунде.
Если возникнут дополнительные вопросы, не стесняйтесь задавать!