Массивное тело подвешено на невесомой и нерастяжимой нити длиной 90 см. Нить с телом отклонили на 600 от вертикали и отпустили. Найти (в м/с) максимальную скорость тела.​

Дано:

l = 90 см = 0,9 м

α = 60°

------------------------------

Найти:

υ(max.) - ?

1) Для начала мы сделаем рисунок про массивное тело подвешено на невесомой и нерастяжимой нити, чтобы было понятно. (Рисунок сделан внизу).

2) Для начала мы воспользуемся законом сохранения энергий, про этого закона мы найдем максимальную скорость тела:

E(понт.) = E(кин.) - закон сохранения энергий

E(понт.) = mgh - потенциальная энергия

E(кин.) = (m×(υ(max.))²)/2 - кинетическая энергия

Следовательно мы получаем:

mgh = (m×(υ(max.))²)/2 | : m

gh = (υ(max.))²/2 | × 2

2gh = (υ(max.))² ⇒ υ(max.) = √(2gh) - максимальная скорость тела (1)

3) Теперь мы еще в условий сказано что нить с телом отклонили на 60° от вертикали и отпустили - это значит что получится прямоугольный треугольник, потому что нить с телом отклонили на 60° от вертикали и отпустили его вниз. По рисунку мы видим что получился прямоугольный треугольник, но нам надо найти высоту которую тело отпустили, следовательно мы получим:

Пусть гипотенуза нерастяжимой нити -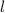 , тогда маленький катет - .

Теперь мы находим высоту, которую указан на рисунке:

- высота которую тело опустили (2)

3) Теперь мы находим общую формулу про максимальную скорость тела пользуясь из (1) и (2), тогда мы получим:

υ(max.) = √(2gh)  и h = l/2, следовательно:

υ(max.) = √(2g × (l/2)) = √(g×l) ⇒ υ(max.) = √(g×l) - максимальная скорость тела

υ(max.) = √(9,8 м/с² × 0,9 м) = √(8,82 м²/с²) ≈ 2,97 м/с

ответ: υ(max.) = 2,97 м/с