1. Физика
  2. Лаб раб-рычаг. как найти

Лаб раб-рычаг. как найти отношение сил и плеч​


Лаб раб-рычаг. как найти отношение сил и плеч​

arianadorofeva arianadorofeva    2   17.04.2021 15:53    0

Ответы
Татьяна201712 Татьяна201712  17.05.2021 15:57

Отношение находится делением одного на другое.

У вас тут два разных отношения (отношение сил и отношение плеч), и для каждого в таблице написано, что на что делить:

- отношение сил: делим силу F₁ на силу F₂

- отношение плеч: делим длину плеча на длину плеча

Несмотря на то, что это два разных отношения, но по свойству рычага, оба эти отношения должны быть равны друг другу.

опыт №1

отношение сил: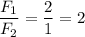  $\frac{F_1}{F_2}=\frac{2}{1}=2

отношение плеч: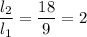  $\frac{l_2}{l_1}=\frac{18}{9}=2

опыт №2

отношение сил: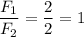  $\frac{F_1}{F_2}=\frac{2}{2}=1

отношение плеч: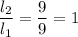  $\frac{l_2}{l_1}=\frac{9}{9}=1

опыт №3

отношение сил: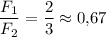  $\frac{F_1}{F_2}=\frac{2}{3}\approx0{,}67

отношение плеч: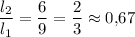  $\frac{l_2}{l_1}=\frac{6}{9}=\frac{2}{3}\approx0{,}67

Всё, записываем все вычисленные значения в таблицу (в третьем опыте можно записать обыкновенной дробью точное значение 2/3 либо десятичной- приближённое значение 0,67 или ещё можно записать в виде бесконечной периодической десятичной дроби 0,(6) если вы такое проходили, конечно).

Как видим, в каждом опыте оба отношения равны друг другу. Что и требовалось доказать.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
классоопп классоопп  02.03.2021 14:20
118. Плавающая деревянная балка вытесняет 0,75 м3 воды, а если она полностью погружена в воду, вытесняет 1 м3 воды. Определите силы отталкивания, действующие на сустав....
098473 098473  02.03.2021 14:20
Выберите положения тела, в которых оно оказывает наибольшее инаименьшее давление наповерхность. Напишите ответ,Используя слова «давление»,«Площадь», «сила».БІ3​...
nadiakrasavtze nadiakrasavtze  02.03.2021 14:20
Человек, сидящий в трамвае, движется относительно * укажите правильный вариант:других пассажировзданийсидений трамваяводителя трамвая​...
1010ВАДИМ 1010ВАДИМ  16.09.2019 16:10
Электрон после разгона в электростатическом поле с разностью потенциалов 500в влетает в однородное магнитное поле с индукцией в=0,2 тл и движется в нем по дуге окружности. определите...
сахарок191 сахарок191  16.03.2021 11:35
Площадь малого поршня (1) равна 4 см2, а площадь большого поршня (2) — 1,1 м2. Поршни находятся в равновесии. Вычисли, во сколько раз сила давления на больший поршень больше силы...
Violetta1508mailru Violetta1508mailru  16.03.2021 11:35
1. При передаче электроэнергии на большое расстояние используют: 1) переменный ток и низкое напряжение; 2)постоянный ток ивысокое напряжение; 3) переменный ток и высокое напряжение;...
ира09н9 ира09н9  16.03.2021 11:36
4.ответы на вопросы по содержанию. 1)Чем увлекался Ю. Гагарин в детстве?2)О чём переживала учительница, глядя на маленького Юру?3) С какой целью шёл инспектор в класс?4)Из-за чего...
saya8282 saya8282  16.03.2021 11:36
11. В опыте обнаружено, что при подъеме проволочной рамки из воды водяная пленка разрывается при значении силы 2,8-10° Н. Каково значение коэффициентаповерхностного натяжения воды,...
zFast88 zFast88  16.03.2021 11:36
СОЧ ЗА 3 ЧЕТВЕРТЬ 7 КЛАСС (даю 25 б)​...
ХлойкаПрайс ХлойкаПрайс  26.02.2019 17:50
.(Найти число n атомов, содержащих в капельке ртути массой m=1г)....

Популярные вопросы