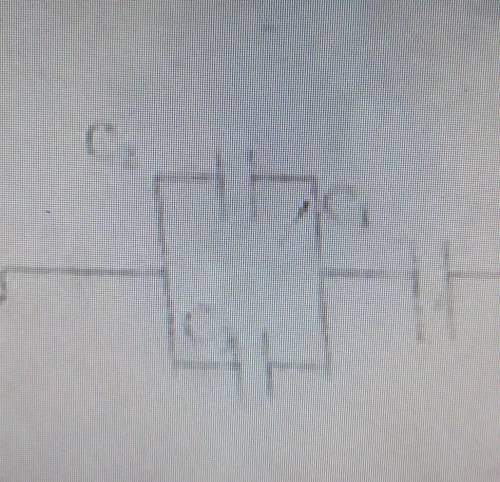
Конденсаторы с емкостями С1=1мкф, С2=2мкф, С3=3мкф соединены как показано на рисунке, напряжение U=12. Определить заряд на конденсаторе С3​

Давай разберем данную задачу шаг за шагом.

У нас есть три конденсатора: С1, С2 и С3, с емкостями 1 мкФ, 2 мкФ и 3 мкФ соответственно, и напряжение между пластинами U=12 В.

Изначально, когда конденсаторы разомкнуты, они не имеют зарядов на своих пластинах. Задача состоит в определении заряда на конденсаторе C3.

Для решения данной задачи, мы можем использовать два основных закона для конденсаторов:

1) Закон сохранения заряда - суммарный заряд, сохраняемый в замкнутой системе, не изменяется. Это означает, что заряд, протекающий через один конденсатор, равен заряду, протекающему через другие конденсаторы в параллельной цепи.

2) Закон сохранения энергии - энергия, сохраняемая в замкнутой системе, также не изменяется. Это означает, что сумма энергий, хранимая в каждом из конденсаторов, равна энергии, хранимой в источнике напряжения U.

Итак, приступим к решению задачи.

1. Первый шаг - рассмотрим параллельное соединение конденсаторов C2 и C3. Когда конденсаторы соединены параллельно, заряды на их пластинах равны. Обозначим этот общий заряд как Q1.

Q1 = заряд на пластинах C2 и C3

Используя формулу для расчета заряда на конденсаторе (Q = C * U), где Q - заряд, C - емкость, U - напряжение, подставим значения для C2 и получим:

Q1 = C2 * U
= 2 мкФ * 12 В
= 24 мкКл

2. Второй шаг - рассмотрим последовательное соединение конденсаторов C1 и C2 + C3. Когда конденсаторы соединены последовательно, напряжение на них одинаково. Обозначим это общее напряжение как U2.

U2 = напряжение на конденсаторах C1, C2 и C3

Так как U2 = U (из условия задачи), мы можем записать:

U = U2 = 12 В

3. Третий шаг - рассчитаем заряд на конденсаторе C2 + C3, используя закон сохранения заряда:

Q2 = Q1 = 24 мкКл

4. Четвертый шаг - рассчитаем заряд на конденсаторе C3, используя закон сохранения заряда:

Q3 = Q1 - Q2
= 24 мкКл - 24 мкКл
= 0 мкКл

Ответ: Заряд на конденсаторе C3 равен 0 мкКл (нет заряда на его пластинах).