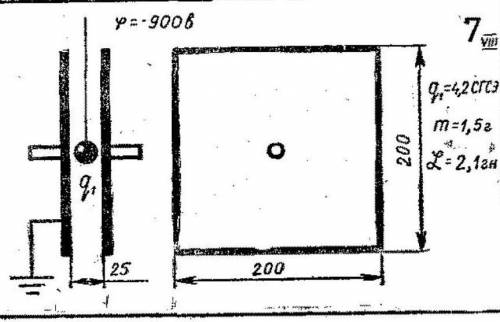
Конденсатор Найти:
1) активную площадь
2) электроёмкость ( в пФ)
3) напряжённость поля между пластинами ( в
Н/Кл)
4) величина заряда на незаземлённой конденсаторной пластине (нКл)
5) с какой силой поле конденсатора действует на заряд q1, величина которого указана на карточке? (
Н)
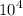
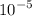
Другие вопросы по теме Физика
Популярные вопросы
- Визначте ступінь тяжкості злочинів у таких правових ситуаціях...
2 - Виведіть формулу вуглеводню, якщо при повному згорянні 0.3 моль цієї речовини...
2 - Складiть i запишiть дiалог(12-14 реплiк) по фото...
1 - Реши систему двух уравнений. ...
2 - Физика 10 класс СОРПри вдвигании в катушку постоянного магнита в ней возникает...
1 - 1) Look out! Hefall! is is going to will 2) What s the weathertoday? like temperature...
3 - Дан квадрат ATMV . T M A V 1. Выполни параллельный перенос квадрата на вектор...
2 - 1. Числівниками є всі слова в рядку А) десять, десятеро, десятка, десятий; Б)...
2 - Напишите рассказ как защитить себя даю. ...
1 - Часть 1. Спишите текст, расставьте недостающие знаки препинания, вставьте пропущенные...
1
1) Для нахождения активной площади конденсатора обратимся к формуле:
C = ε₀ * S / d,
где C - электроёмкость конденсатора, ε₀ - электрическая постоянная (ε₀ ≈ 8,85 * 10^(-12) Ф/м), S - площадь пластин конденсатора, d - расстояние между пластинами.
По условию задачи, электроемкость C = 100 пФ, а расстояние между пластинами d = 1 мм = 0,001 м.
Подставляя данные в формулу, получаем: 100 * 10^(-12) = 8,85 * 10^(-12) * S / 0,001
Домножая обе части уравнения на 0,001, получаем: S = 100 * 10^(-12) * 0,001 / 8,85 * 10^(-12) = 0,113 м²
Ответ: активная площадь конденсатора равна 0,113 м².
2) Для нахождения электроёмкости конденсатора, обратимся к формуле:
C = ε₀ * S / d,
где C - электроёмкость конденсатора, ε₀ - электрическая постоянная (ε₀ ≈ 8,85 * 10^(-12) Ф/м), S - активная площадь пластин конденсатора, d - расстояние между пластинами.
Подставляя значения в формулу, получаем: C = 8,85 * 10^(-12) * 0,113 / 0,001 = 8,85 пФ
Ответ: электроёмкость конденсатора равна 8,85 пФ.
3) Для нахождения напряжённости поля между пластинами обратимся к формуле:
E = U / d,
где E - напряжённость поля, U - напряжение между пластинами, d - расстояние между пластинами.
По условию задачи, напряжение U = 10^4 В, а расстояние между пластинами d = 1 мм = 0,001 м.
Подставляя значения в формулу, получаем: E = 10^4 / 0,001 = 10^7 Н/Кл
Ответ: напряжённость поля между пластинами равна 10^7 Н/Кл.
4) Для нахождения величины заряда на незаземлённой конденсаторной пластине, используем формулу:
Q = C * U,
где Q - заряд на пластине, C - электроёмкость конденсатора, U - напряжение между пластинами.
Подставляя значения в формулу, получаем: Q = 8,85 * 10^(-12) * 10^4 = 8,85 * 10^(-8) Кл = 88,5 нКл
Ответ: величина заряда на незаземлённой конденсаторной пластине равна 88,5 нКл.
5) Для нахождения величины силы, с которой поле конденсатора действует на заряд q1, воспользуемся формулой:
F = q1 * E,
где F - сила, q1 - величина заряда, E - напряжённость поля.
Подставляем значения в формулу: F = (10^(-5)) * (10^7) = 10^2 Н
Ответ: сила, с которой поле конденсатора действует на заряд q1, равна 10^2 Н.