Катушка с индуктивностью L=0.18 Гн и с активным сопротивлением R=30 Ом последовательно с конденсатором ёмкостью C=40 мкф подключена к источнику с напряжением U=250sin500t В.
Написать выражения тока в цепи и напряжение на конденсаторе. Определить показания вольтметра

Для решения данной задачи, нам необходимо воспользоваться законами Кирхгофа и иметь знания о взаимодействии индуктивности и конденсатора в электрической цепи.

Для начала, запишем уравнение для напряжения на конденсаторе:
u(t) = Umax * sin(ωt), где Umax - максимальное значение напряжения на источнике, ω - угловая частота, t - время.

Затем нам необходимо определить выражения для тока, текущего по цепи. Мы можем разделить цепь на два элемента - индуктивность и активное сопротивление.

Определим выражение для реактивного сопротивления катушки:
XL = ωL, где ω - угловая частота, L - индуктивность (генри).

Определим выражение для реактивного сопротивления конденсатора:
XC = 1 / (ωC), где ω - угловая частота, C - ёмкость (фарад).

Общее импеданс цепи можно определить, сложив реактивные сопротивления конденсатора и катушки в квадрате, а затем извлекая из них квадратный корень:
Z = √(R^2 + (XL - XC)^2)

Далее, для определения текущего тока I в цепи, мы можем использовать закон Ома:
I = Umax / Z

Теперь, чтобы определить выражение для тока, проходящего через эту цепь, мы можем использовать фазовый угол φ:
tan(φ) = (XL - XC) / R

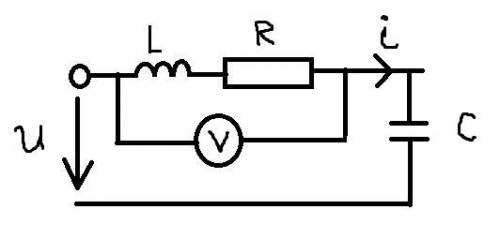
Графическое изображение данной цепи показано на рисунке.

Шаги решения задачи:

1. Записываем уравнение для напряжения на источнике: u(t) = 250 * sin(500t).
2. Определяем угловую частоту: ω = 2πf, где f - частота, равная 500 Гц.
3. Рассчитываем реактивное сопротивление катушки: XL = ωL.
XL = (2π * 500) * 0.18 = 564 Ом.
4. Рассчитываем реактивное сопротивление конденсатора: XC = 1 / (ωC).
XC = 1 / ((2π * 500) * 40 * 10^(-6)) = 198 Ом.
5. Определяем общий импеданс цепи: Z = √(R^2 + (XL - XC)^2).
Z = √((30)^2 + (564 - 198)^2) = √(900 + 366624) = 606 Ом.
6. Рассчитываем фазовый угол φ: tan(φ) = (XL - XC) / R.
tan(φ) = (564 - 198) / 30 = 12.2.
φ = tan^(-1)(12.2) ≈ 86.2 градусов.
7. Определяем выражение для тока в цепи: I = Umax / Z.
I = 250 / 606 ≈ 0.412 А.
8. Записываем выражение для тока: i(t) = 0.412 * sin(500t - 86.2°).
9. Определяем выражение для напряжения на конденсаторе: uC(t) = Umax * sin(ωt + φ).
uC(t) = 250 * sin(500t + 86.2°).

10. Для определения показаний вольтметра необходимо рассчитать напряжение на конденсаторе в момент времени t = 0, так как вольтметр показывает мгновенные значения. Подставляя t = 0 в уравнение для напряжения на конденсаторе, получаем:
uC(0) = 250 * sin(0 + 86.2°) ≈ 237 В.

Таким образом, выражение для тока в цепи: i(t) = 0.412 * sin(500t - 86.2°), а показания вольтметра в начальный момент времени будут приближенно равны 237 В.