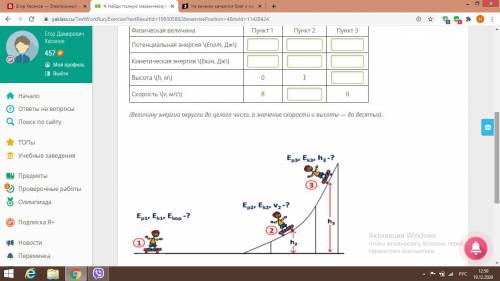
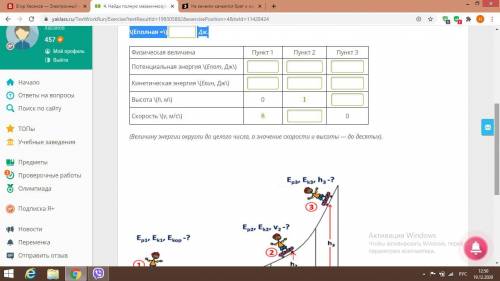
Катание на скейтборде по рампе напрямую связано с законом сохранения полной механической энергии. Более высокая скорость движения всегда достигается в более низкой точке рампы. На рисунке показана модель рампы в скейт-парке. Общая масса скейтера со скейтбордом (роликовой доской) равна 78 кг. Ускорение свободного падения принять равным 10 мс2 и силу сопротивления движению не учитывать.

Используя данные величины, заполни таблицу до конца.
Какова полная механическая энергия скейтера со скейтбордом?

\(Eполная =\)
Дж.

пРККПЦУПквввыы пппвййййвв аааарпр прпрп

Для решения этой задачи мы будем использовать закон сохранения полной механической энергии, который гласит, что сумма кинетической и потенциальной энергии остается постоянной в отсутствие внешних сил (как в данном случае силы сопротивления движению).

Для начала, нам нужно вычислить потенциальную энергию скейтера в самой верхней точке рампы. Для этого мы будем использовать формулу:

\(E_{пот} = m \cdot g \cdot h\),

где \(m\) - масса скейтера со скейтбордом, \(g\) - ускорение свободного падения (равное 10 м/с^2) и \(h\) - высота рампы.

По рисунку мы видим, что высота рампы равна 2 м, поэтому:

\(E_{пот} = 78 \, \text{кг} \cdot 10 \, \text{м/с}^2 \cdot 2 \, \text{м} = 1560 \, \text{Дж}\).

Теперь нам нужно вычислить кинетическую энергию скейтера в самой низкой точке рампы. Формула для этого:

\(E_{кин} = \frac{1}{2} \cdot m \cdot v^2\),

где \(m\) - масса скейтера со скейтбордом и \(v\) - скорость скейтера в низшей точке рампы.

Мы знаем, что скорость движения скейтера в низшей точке равна максимальной. Чтобы вычислить эту максимальную скорость, мы можем использовать закон сохранения энергии:

\(E_{полная} = E_{пот} + E_{кин}\).

Подставим известные значения в эту формулу:

\(E_{полная} = 1560 \, \text{Дж} + E_{кин}\).

Нам нужно найти \(E_{полная}\), поэтому оставим ее неизвестной.

Теперь выразим \(E_{кин}\) через \(E_{полная}\):

\(E_{кин} = E_{полная} - 1560 \, \text{Дж}\).

Двигаясь дальше, мы записываем выражение для кинетической энергии:

\(E_{кин} = \frac{1}{2} \cdot m \cdot v^2\).

Подставим выражение для \(E_{кин}\) в это уравнение:

\(E_{полная} - 1560 \, \text{Дж} = \frac{1}{2} \cdot m \cdot v^2\).

Теперь мы можем решить это уравнение относительно \(v\):

\(v^2 = \frac{2 \cdot (E_{полная} - 1560 \, \text{Дж})}{m}\).

И, наконец, найдем значение \(v\):

\(v = \sqrt{\frac{2 \cdot (E_{полная} - 1560 \, \text{Дж})}{m}}\).

Ответом на вопрос является значение полной механической энергии скейтера со скейтбордом, которое требуется вычислить по формуле:

\(E_{полная} = E_{пот} + E_{кин}\),

где \(E_{пот} = 1560 \, \text{Дж}\) и \(E_{кин} = \frac{1}{2} \cdot m \cdot v^2\), а \(v\) вычисляется по формуле \(v = \sqrt{\frac{2 \cdot (E_{полная} - 1560 \, \text{Дж})}{m}}\).