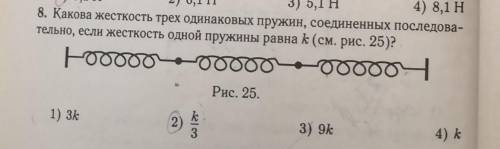
Какова жесткость трёх одинаковых пружин, соединённых последовательно, если жесткость одной пружины равна k? ответ: k/3. Как получить такой результат?
Другие вопросы по теме Физика
Популярные вопросы
- 3) Найди верное утверждение: А) вода содержится в каждой клеточке нашего...
2 - Розкрий зміст прислівя ,,Бережи честь з молоду,,...
3 - ответьте надо 1. Когда к власти пришла партия Большевиков: А) 7ноября...
3 - Сделайте краткий конспект по презентации https://mypresentation.ru/presentation/otdelka-zhilogo-pomeshheniya...
3 - Найдите в этом тексте предложение с вводным словом: 1.Летний день угасает,...
2 - Продолжи последовательность чисел составленную по некоторому провилу...
3 - Что такое киномузыка? и какой вклад в киномузыку внёс композитор И....
1 - Через невесомый блок перекинута невесомая нерастяжимая нить на которой...
3 - Який спектр випромінює нитка розжарення електричної лампи у нормальному...
3 - 295 : 21. Выполни действие и вырази делимое через неполное частное,...
2
Объяснение:
мы растягиваем набор пружин с силой F
эту силу мы прикладываем ко всем трем пружинам и все они растягиваются
пружина 1 растянулась на х так что к*х= F
пружина 2 растянулась на х так что к*х= F
пружина 3 растянулась на х так что к*х= F
в итоге три пружины растянулись под действием силы F на расстояние 3х
значит жесткость этой системы равна K=F/(3x)
мы знаем что для одной пружины F=k*x тогда K=F/(3x)= k/3
Когда пружины соединены последовательно, то они работают как одна общая пружина, их жесткости складываются. Таким образом, чтобы рассчитать жесткость системы из трех пружин, мы должны сложить жесткости каждой отдельной пружины.
Пусть жесткость одной пружины равна k, и мы хотим найти жесткость системы из трех одинаковых пружин.
1. Жесткость системы трех пружин равна сумме жесткостей каждой пружины. В нашем случае, это k + k + k = 3k.
2. Однако, нам нужно найти жесткость только одной пружины в системе. Для этого мы должны разделить общую жесткость системы на количество пружин в ней.
жесткость одной пружины = общая жесткость системы / количество пружин
= 3k / 3
= k
Таким образом, получаем, что жесткость одной пружины в системе трех одинаковых пружин, соединенных последовательно, равна k/3.