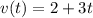Как найти V(t), если S(t) = 2t+1,5t^2, а X0 = 2м?
Другие вопросы по теме Физика
Популярные вопросы
- Задача 1. По предложенной последовательности нуклеотидов в информационной...
1 - Переріз, що проходить через вершину конуса, утворює з площиною основи...
3 - До іть будь ласка Діаметер циліндра 3 см висота ✓3.Знайдіть кут між діаноналлю...
1 - Перечислите разделения смесей. Какие свойства компонентов лежат в основе...
1 - длина дороги 657км. длина пути,проделанного туристом во 2-ой день в 5...
1 - Ценности казахского народа...
1 - 1) -0,4x’y(3xy²-70xy+15 x+y);...
3 - За время t=0.075 c точка поверхности барабана стиральной машины полукруг...
1 - График поступков гринёва в Капитанской дочке...
3 - (2 2/3- 2 2/9)×(2 - 1 1/2)=???...
2
Первый физический смысл производной)
Скорость — первая производная перемещения от времени: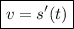
Значит,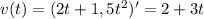
Также скорость — первая производная координаты от времени: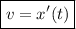 Здесь
Здесь 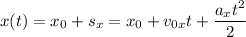
Значит, из уравнения координаты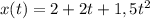 имеем:
имеем: 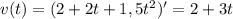
Второй с формул)
Перемещение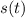 при равноускоренном прямолинейном движении можно определить по формуле
при равноускоренном прямолинейном движении можно определить по формуле 
Из этой формулы имеем: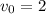 м/с и
м/с и 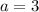 м/с²
м/с²
Тогда из определения ускорения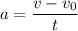 имеем:
имеем: 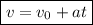
Подставляем значения: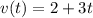
ответ: