Как изменится частота колебаний нитяного маятника длиной 0,5 м, если увеличить длину нити 1,5 м? с решение
Другие вопросы по теме Физика
Популярные вопросы
- Какой этап характерен для уроков технического моделирования:...
3 - Аттестация с целью подтверждения соответствия занимаемой должности проводится...
1 - По методике оценки квалификации аттестуемых педагогических работников под...
1 - По В.Д. Шадрикову, в структуру педагогической компетентности в области личностных...
2 - Новым подходом в воспитании детей является:...
1 - Какое государственное учреждение осуществляет регулирование занятости населения:...
3 - Имеют ли право обучающиеся, воспитанники гражданских образовательных учреждений...
2 - По методике О.С. Газмана, этапы деятельности по педагогической поддержке...
3 - Основной процедурой аттестации с целью установления соответствия уровня квалификации...
1 - Что такое профессиональная пригодность?...
3
По формуле периода колебаний математического маятника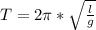
l - длина маятника (м), g - ускорение свободного падения (g = 10 м/с²), T - период колебаний (с). Связь периода и частоты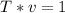 ⇒
⇒ 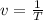 (v
(v -частота колебаний (Гц)). Заменим период частатой в формуле периода математического маятника
-частота колебаний (Гц)). Заменим период частатой в формуле периода математического маятника 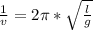
Частота маятников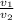 = 14 . Частота маятника длиной 0,5 метров больше частоты маятника длиной 2 метра в 14 раз.
= 14 . Частота маятника длиной 0,5 метров больше частоты маятника длиной 2 метра в 14 раз.