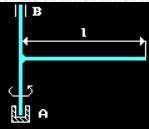
К валу AB жестко прикреплен горизонтальный однородный стержень длиной l = 1.7 м, имеющий массу m = 3.7 кг. Валу сообщена угловая
скорость ω = 11 рад/с. Предоставленный самому себе, он остановился,
сделав 40 оборотов. Определите момент трения в подшипниках,
считая его постоянным.

Для решения данной задачи мы будем использовать законы сохранения механической энергии и уравнение моментов.

Первым шагом определим кинетическую энергию вращения вала. Кинетическая энергия вращения тела определяется формулой:

К = (1/2) * I * ω^2,

где К - кинетическая энергия, I - момент инерции тела относительно оси вращения, ω - угловая скорость.

Момент инерции стержня относительно оси вращения, проходящей через его конец (то есть точку А), можно найти по формуле:

I = (1/3) * m * l^2,

где m - масса стержня, l - его длина.

Подставляя данные в эти формулы, получаем:

I = (1/3) * 3.7 кг * (1.7 м)^2 = 4.725 кг * м^2.

К = (1/2) * (4.725 кг * м^2) * (11 рад/с)^2 = 289.8275 Дж.

Далее, применим закон сохранения механической энергии. Поскольку вал вышел самостоятельно из движения, его полная механическая энергия в начальный и конечный моменты равны:

K_begin + U_begin = K_end + U_end,

где K_begin и K_end - кинетическая энергия в начальный и конечный моменты, U_begin и U_end - потенциальная энергия в начальный и конечный моменты.

Так как в начальный момент вал подвижен и совершает 40 оборотов, то его кинетическая энергия равна нулю (все энергия перешла в потенциальную), а потенциальная энергия может быть найдена по формуле:

U_begin = m * g * h_begin,

где m - масса вала, g - ускорение свободного падения, h_begin - высота начальной точки относительно точки опоры.

В конечный момент вал остановился и его потенциальная энергия равна нулю, а кинетическая энергия равна рассчитанной ранее.

Таким образом, получаем:

m * g * h_begin = 289.8275 Дж.

h_begin = 289.8275 Дж / (m * g).

Подставляя значения, получаем:

h_begin = 289.8275 Дж / (3.7 кг * 9.8 м/с^2) = 8.279 м.

Далее, рассчитаем момент трения в подшипниках. Момент трения в подшипниках определяется как произведение радиуса шарнира х силы трения, приложенной в нем. Вращающий момент, созданный силой трения, равен моменту силы трения:

M_friction = R * F_friction,

где M_friction - момент трения в подшипниках, R - радиус шарнира (дано на рисунке), F_friction - сила трения.

Рассмотрим теперь равновесие пытки (стержня). Проекция веса стержня на ось AB равна:

F_weight = m * g * cos(α),

где α - угол между горизонталью и стержнем.

Сила трения равна проекции веса стержня на радиус шарнира:

F_friction = m * g * cos(α) * R.

Подставляя значения, мы получаем:

F_friction = 3.7 кг * 9.8 м/с^2 * cos(α) * 0.3 м.

8) 100144 --7

Таким образом, момент трения в подшипниках составляет:

M_friction = 0.3 м * 3.7 кг * 9.8 м/с^2 * cos(α) * 0.3 м = 3.215 Н * м * cos(α).

Ответ: момент трения в подшипниках составляет 3.215 Н * м * cos(α).