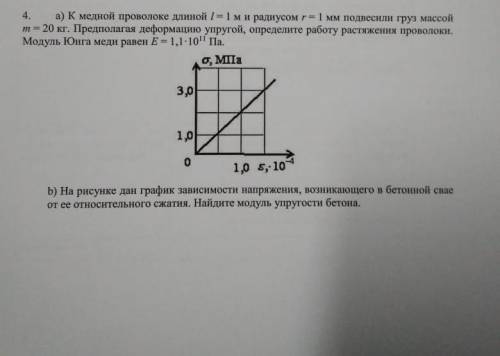
К медной проволоке длиной l= 1 м и радиусом r= 1 мм подвесили груз массой m= 20 кг. Предполагая деформацию упругой, определите работу растяжения проволоки. Модуль Юнга меди равен E=1,1*10^11Па.
Другие вопросы по теме Физика
Популярные вопросы
- Выберите из списка деятеля Возрождения, не являющегося итальянцем....
1 - Составьте 5 задач на второй закон Менделя и 5 задач на третий закон...
2 - Опір провідника дорівнює 1 Ом . що це означає?...
2 - РАССТАВЬТЕ ЗАРЯД ИОНОВ CO2...
2 - Первичная катушка трансформатора имеет 1000 витков. На тот же сердечник...
2 - А.П Шестаков, 1994 год Решите быстро. https://yagubov.ru/math/41-1-0-5981...
1 - 1. Вычислите: 1) 0,036 - 3,5; 2) 37,53 1 000; 3) 3,68 - 0,01; 2....
3 - Думаю что , фамилия автора любит не любит родной край потому что...
3 - Оксид железа(II) в отличие от оксида железа(III) взаимодействует...
3 - Найдите 1/корень из 7 косинус альфа/2, если косинус альфа равен -11/25,...
2
работа = (1/2) * k * Δx^2,
где k - коэффициент упругости проволоки, Δx - изменение длины проволоки.
Сначала нам необходимо найти коэффициент упругости проволоки. Коэффициент упругости проволоки связан с модулем Юнга следующим образом:
k = (π * r^2 * E) / l,
где r - радиус проволоки, E - модуль Юнга материала проволоки, l - длина проволоки.
Подставляя значения в формулу, получаем:
k = (π * (0.001 м)^2 * 1.1 * 10^11 Па) / 1 м = 3.43 * 10^8 Н/м.
Теперь мы можем найти изменение длины проволоки (Δx). Изменение длины проволоки можно найти, используя закон Гука:
Δx = (F * l) / (π * r^2 * E),
где F - сила, действующая на проволоку.
Сила, действующая на проволоку, равна массе груза, умноженной на ускорение свободного падения:
F = m * g,
где m - масса груза (20 кг), g - ускорение свободного падения (около 9,8 м/с^2).
Подставляя значения в формулу, получаем:
F = (20 кг) * (9.8 м/с^2) = 196 Н.
Δx = (196 Н * 1 м) / (π * (0.001 м)^2 * 1.1 * 10^11 Па) ≈ 0.053 м.
Теперь, используя найденное значение Δx и коэффициент упругости k, мы можем найти работу растяжения проволоки:
работа = (1/2) * k * Δx^2 = (1/2) * (3.43 * 10^8 Н/м) * (0.053 м)^2 ≈ 4.57 Дж.
Таким образом, работа растяжения проволоки составляет около 4.57 Дж (джоуля). Это означает, что энергия, затраченная на растяжение проволоки, равна 4.57 Дж.