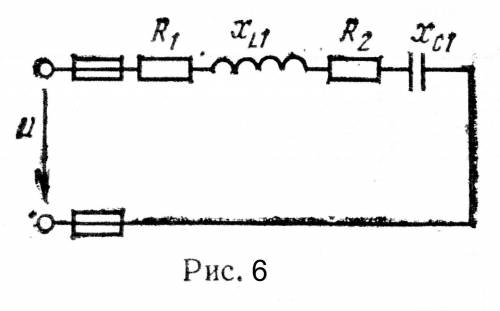
Известны: R1=6 Ом; R2=2 Ом; XL1=3 Ом; XC1=9Ом; U=40 В. Определить: 1) полное сопротивление Z; 2) ток I; 3) угол сдвига фаз φ; 4) активную P, реактивную Q и полную S мощности цепи.

Начертить в масштабе векторную диаграмму цепи и пояснить её построение

Для решения данной задачи, нам понадобятся некоторые формулы для расчета электрической цепи, а именно закон Ома (I = U/Z) и формулы для расчета полной, активной и реактивной мощностей (P = U * I * cos(φ), Q = U * I * sin(φ), S = U * I).

Шаг 1: Расчет полного сопротивления Z
Зная значения сопротивлений R1 и R2, а также реактивных сопротивлений XL1 и XC1, можем рассчитать полное сопротивление Z по формуле:
Z = sqrt[(R1 + R2)^2 + (XL1 - XC1)^2]
= sqrt[(6 + 2)^2 + (3 - 9)^2]
= sqrt[64 + 36]
= sqrt[100]
= 10 Ом

Ответ: Полное сопротивление Z равно 10 Ом.

Шаг 2: Расчет тока I
Используя закон Ома, можем выразить ток I:
I = U / Z
= 40 / 10
= 4 А

Ответ: Ток I равен 4 А.

Шаг 3: Расчет угла сдвига фаз φ
Угол сдвига фаз φ можно рассчитать по формуле:
φ = arctan((XL1 - XC1) / (R1 + R2))
= arctan((3 - 9) / (6 + 2))
= arctan((-6) / 8)
≈ -36.87°

Ответ: Угол сдвига фаз φ примерно равен -36.87°.

Шаг 4: Расчет активной P, реактивной Q и полной S мощностей цепи
Активная мощность P:
P = U * I * cos(φ)
= 40 * 4 * cos(-36.87°)
≈ 137.15 Вт

Реактивная мощность Q:
Q = U * I * sin(φ)
= 40 * 4 * sin(-36.87°)
≈ -91.43 ВАр

Полная мощность S:
S = U * I
= 40 * 4
= 160 ВА

Ответ: Активная мощность P примерно равна 137.15 Вт, реактивная мощность Q примерно равна -91.43 ВАр, а полная мощность S равна 160 ВА.

Для построения векторной диаграммы цепи, укажем направление тока I вдоль оси x и укажем направление напряжения U вдоль оси y. Затем построим прямоугольный треугольник, где гипотенуза будет равна полному сопротивлению Z, основание будет равно активной мощности P, а высота будет равна реактивной мощности Q. Угол между гипотенузой и основанием треугольника будет равен углу сдвига фаз φ.

Данная диаграмма демонстрирует, как электрический ток и напряжение связаны между собой в данной цепи и визуально показывает, какая часть мощности является активной, а какая - реактивной.