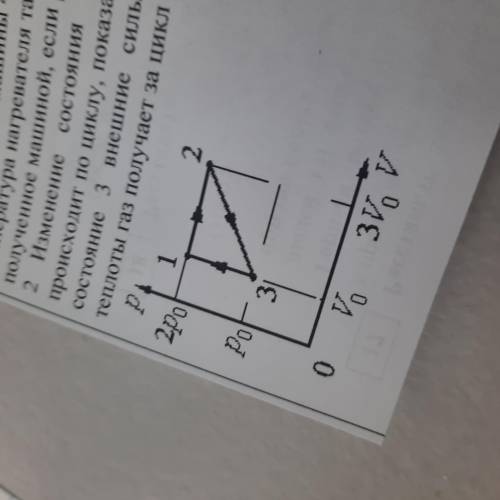
изменение состояния постоянной массы одноатомного идеального газа происходит по циклу, показанному на рисунке. При переходе газа из состояния 2 в состояние 3 внешние силы совершают работу а23 =5кДж. Какое количество теплоты газ получает за цткл от нагревателя?

Для решения этой задачи, нам потребуется знание первого закона термодинамики, который утверждает, что изменение внутренней энергии газа равно сумме работы, совершенной над газом внешними силами и количеством полученной газом теплоты.

Перейдем к анализу цикла изображенного на рисунке. На рисунке видно, что газ проходит через следующие состояния:

1) Из состояния 1 в состояние 2:
Здесь не указана работа и теплота, поэтому мы не можем использовать эту часть цикла для решения задачи.

2) Из состояния 2 в состояние 3:
Здесь указана работа a23 = 5 кДж, которую совершают внешние силы при переходе газа из состояния 2 в состояние 3.

3) Из состояния 3 в состояние 1:
Здесь не указана работа и теплота, но мы знаем, что цикл является замкнутым, поэтому работа, совершенная внешними силами при этом переходе, должна быть равна противоположной работе, совершенной внешними силами при переходе из состояния 1 в состояние 2.

Теперь мы можем использовать первый закон термодинамики, чтобы найти количество полученной газом теплоты за цикл. Формула будет выглядеть следующим образом:

Q_цкл = W_a23 + W_a31,

где Q_цкл - количество теплоты, полученное газом за цикл,
W_a23 - работа, совершенная внешними силами при переходе газа из состояния 2 в состояние 3,
W_a31 - работа, совершенная внешними силами при переходе газа из состояния 3 в состояние 1.

Мы уже знаем, что W_a23 = 5 кДж. Теперь нам нужно найти W_a31.

Работа, совершенная внешними силами при переходе газа из состояния 3 в состояние 1, равна противоположной работе (W_a23) и она также равна изменению внутренней энергии газа при этом переходе.

Теперь нам нужно доказать, что изменение внутренней энергии газа при переходе из состояния 3 в состояние 1 равно W_a23.

Одноатомный идеальный газ подчиняется уравнению состояния, известному как уравнение Пуассона:

U = (3/2)nRT,

где U - внутренняя энергия газа,
n - количество вещества газа (в молях),
R - универсальная газовая постоянная,
T - температура газа.

Учитывая, что газ остается одним и тем же веществом во всех состояниях цикла, мы можем полагать, что nR является постоянным значением. Таким образом, изменение внутренней энергии газа при переходе из состояния 3 в состояние 1 равно разности внутренних энергий в этих состояниях:

ΔU = U_1 - U_3 = (3/2)nRT_1 - (3/2)nRT_3 = (3/2)nR(T_1 - T_3),

где ΔU - изменение внутренней энергии,
T_1 и T_3 - температуры газа в состояниях 1 и 3 соответственно.

Изнутри изображения на рисунке, мы видим, что температура газа в состоянии 3 выше, чем в состоянии 1 (T_3 > T_1), следовательно, ΔU > 0. Это означает, что изменение внутренней энергии газа при переходе из состояния 3 в состояние 1 положительное и равно W_a23:

ΔU = W_a23.

Теперь мы знаем, что W_a31 = -W_a23 = -5 кДж (работа теплообмена с газом).

Возвращаясь к изначальной формуле:

Q_цкл = W_a23 + W_a31 = 5 кДж + (-5 кДж) = 0.

Таким образом, количество теплоты, которое газ получает за цикл от нагревателя, равно нулю.