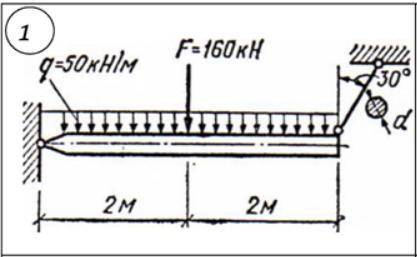
Из условия прочности при растяжении и сжатии, подобрать требуемые размеры поперечного сечения стержня, приняв допускаемое нормальное напряжение 120 Мпа

Объяснение:

у меня ещё нет физики я бы

Для решения данной задачи нам необходимо использовать принципы прочности при растяжении и сжатии материалов. Принцип прочности говорит о том, что допускаемое напряжение в материале не должно превышать предел прочности материала. В данном случае, предел прочности равен 120 Мпа (мегапаскалям).

Первым шагом необходимо определить растягивающее напряжение в стержне. Растягивающее напряжение возникает при растягивании материала и вычисляется по формуле:

σ = F / A

где σ - напряжение, F - сила, которая действует на стержень, A - площадь поперечного сечения стержня.

В данной задаче сила не указана, поэтому предположим, что сила равна 1 кН (килоньтонне), что составляет 1000 Н (ньютонов).

Подставляя известные значения в формулу, получаем:

120 МПа = 1000 Н / A

Раскрывая единицы измерения, получаем:

120 МПа = 1000 Н / (мм^2) * A

Далее, для решения уравнения нужно выразить A. Для этого умножим обе части уравнения на A и поделим на 120 МПа:

A = (1000 Н / (мм^2)) / 120 МПа

Раскрывая единицы измерения и упрощая выражение, получаем:

A = (1000 Н/мм^2) / (120 МПа)

Сокращаем единицы измерения:

A = (1000 / 120) мм

Выполняем арифметическое вычисление:

A ≈ 8,33 мм^2

Таким образом, чтобы стержень оставался в пределах допускаемого напряжения в 120 МПа, необходимо выбрать поперечное сечение стержня, равное приблизительно 8,33 мм^2.

В случае сжатия, принцип остается таким же, только знак напряжения меняется. То есть, напряжение сжатия также должно быть меньше или равно 120 МПа. Поэтому, при использовании данного стержня в сжатом состоянии, его поперечное сечение также должно быть 8,33 мм^2.