Из города на запад отправился велосипедист со скоростью 20 км/ч, а через 3 ч в том же самом направлении выехал автомобиль со скоростью 80 км/ч. через какое время после выезда велосипедиста и на каком расстоянии от харькова автомобилист догонит велосипедиста?

Ответы

rakrak2016 02.10.2020 02:08

Дано:

$v_{1} = 20$ км/ч

$v_{2} = 80$ км/ч

$\tau = 3$ ч

Найти: $t - ? \ x - ?$

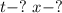
Решение. В системе отсчета "земля" начало координат свяжем с городом, откуда отправились оба тела, а начало отсчета времени — с началом движения велосипедиста.

Согласно условию автомобиль двигался на время $\tau$ меньше, чем велосипедист. Таким образом, уравнение их движения будут иметь вид:

$\left \{ {\bigg{x_{1} = v_{1}t \ \ \ \ \ \ \ \ } \atop \bigg{x_{2} = v_{2}(t - \tau)}} \right.$

В тот момент, когда автомобилист догонит велосипедиста, они будут находиться в одной точке (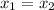 $x_{1} = x_{2}$ ).

Имеем систему уравнений, левые части которых равны, а следовательно, и правые части равны, т. е.

$v_{1}t = v_{2}(t - \tau)$

Отсюда выразим время :

$t = \dfrac{v_{2}\tau}{v_{2} - x_{1}}$

Определим значение искомой величины:

$t = \dfrac{80 \cdot 3}{80 - 20} = 4$ ч

Определим расстояние встречи автомобилиста и велосипедиста (момент, когда автомобилист начнет перегонять велосипедиста).

аналитический).

Расстояние, на котором автомобилист догонит велосипедиста, равняется их общей координате. Найдем ее как координату велосипедиста:

$x = x_{1} = v_{1}t = 20 \cdot 4 = 80$ км

графический).

Запишем уравнения движения (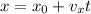 $x = x_{0} + v_{x}t$ ) велосипедиста и автомобиля:

$x_{1} = 20t\\x_{2} = 80(t-3)$

Построим их графики (смотрите вложение). Точка пересечения графиков будет определять координату места, где автомобиль догонит велосипедиста, и время, когда это произойдет.

ответ: автомобиль догонит велосипедиста через 4 ч после выезда велосипедиста на расстоянии 80 км от города.