Идеальный газ, состоящий из N молекул, дипольный момент каждой из которых р помещен в однородное электрическое поле напряженностью E. Вычислите величину
вектора поляризации газа. Температура газа Т.

Ответы

эд104267 15.10.2020 15:57

Потенциальная энергия одного дипольчика во внешнем электрическом поле равна

$E_p= -(\mathbf{p}\cdot\mathbf{E}) = -pE\cos\alpha$

Где α - угол между диполем и внешним полем (может быть от нуля до 180)

Будем полагать, что в равновесном состоянии распределение диполей по энергиям задается распределением Больцмана:

$w(E_p) = C\exp(-E_p/kT)$ ,

Где C - некая нормировочная константа

Перейдем от распределения по энергиям к распределению по переменной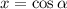 $x = \cos\alpha$

$\displaystyle\\w(x) = w(E_p(x))\left|\frac{dE_p}{dx}\right| = CpE\exp(pEx/kT) = C_1\exp(pEx/kT)$

Найдем новую нормировочную константу C_1

$\displaystyle\int\limits_{-1}^1C_1\exp(pEx/kT)dx = 1\\C_1kT/pE\cdot[\exp(pE/kT)-\exp(-pE/kT)] = 1\\C_1 = \frac{pE}{2kT\sinh(pE/kT)}$

sinh - гиперболический синус.

Найдем средний косинус угла, который составляют диполные моменты молекул с полем

$\displaystyle\langle x \rangle = \int\limits_{-1}^1xC_1\exp(pEx/kT)dx = \\C_1\left(\frac{kT}{pE}\right)^2\int\limits_{-pE/kT}^{pE/kT}u\exp(u)du = \\C_1\left(\frac{kT}{pE}\right)^2\left[\exp(pE/kT)(pE/kT-1) - \exp(-pE/kT)(-pE/kT-1)\right] = \\2C_1\left(\frac{kT}{pE}\right)^2\left[\frac{pE}{kT}\cosh\frac{pE}{kT}-\sinh\frac{pE}{kT}\right] = \coth\frac{pE}{kT}-\frac{kT}{pE}$

Так как задача симметрична относительно вращений вокруг вектора поля E, средний дипольный момент газа будет иметь ненулевую проекцию только на направление этого вектора. Проекция усредненного вектора поляризации газа на это направление, соответственно, равна

$\displaystyle\\P = \frac{pN\langle x\rangle}{V} = \frac{pN}{V}\left[\coth\frac{pE}{kT} - \frac{kT}{pE}\right]$