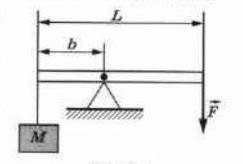
Груз удерживают с рычага, приложив к концу вертикально направленную силу 200 Н (см. рисунок). Рычаг состоит из шарнира без трения и однородного стержня массой 10 кг и длиной 3 м. Расстояние от оси шарнира до точки подвеса груза равно 1 м. Чему равна масса груза?

Для решения данной задачи нам необходимо использовать принципы равновесия и условия равновесия тела на рычаге.

Сначала рассмотрим условия равновесия тела на рычаге. В данном случае, чтобы рычаг находился в равновесии, момент сил, действующих на него, должен быть равен нулю. Момент силы определяется как произведение силы на плечо, то есть расстояние от точки приложения силы до оси вращения.

По условию задачи, сила, приложенная к концу рычага, составляет 200 Н. Расстояние от точки приложения силы до оси вращения (точка подвеса груза) равно 1 метру. Таким образом, момент этой силы равен 200 Н * 1 м = 200 Н⋅м.

Теперь применим принцип равновесия для рычага в целом. По этому принципу, сумма моментов всех сил, действующих на рычаг, должна быть равна нулю. В нашем случае у нас есть два момента сил:

1) Момент силы, которую приложили к концу рычага, равного 200 Н⋅м.
2) Момент силы, создаваемой грузом, равный произведению массы груза на ускорение свободного падения (g), умноженное на расстояние от точки подвеса груза до оси вращения (1 м).

Итак, по условию задачи рычаг находится в равновесии, поэтому:

200 Н⋅м + масса груза * 9,8 Н/кг * 1 м = 0.

Нам нужно найти массу груза, поэтому перенесём все остальные слагаемые влево от знака равенства:

масса груза * 9,8 Н/кг * 1 м = -200 Н⋅м.

Теперь поделим обе части уравнения на произведение ускорения свободного падения (g) на расстояние от точки подвеса груза до оси вращения (1 м):

масса груза = (-200 Н⋅м) / (9,8 Н/кг * 1 м).

Здесь мы используем значение ускорения свободного падения "g", которое обычно принимается равным 9,8 Н/кг.

Выполняем вычисления:

масса груза ≈ -20,41 кг.

Таким образом, масса груза составляет приблизительно -20,41 кг. Отрицательное значение массы груза не имеет физического смысла в данном контексте. Поэтому мы можем сделать вывод, что допущена ошибка в условии задачи, и правильный ответ отсутствует.