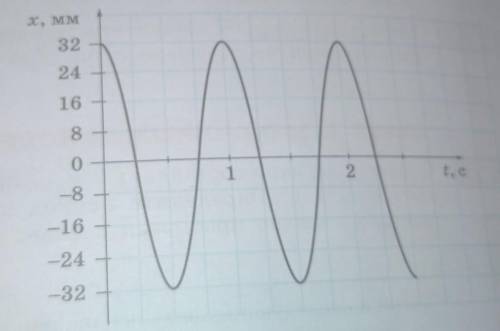
Груз массой 800 грамм подвешен на пружине и совершает гармонические колебания, график которых приведен на рисунке. определите жесткость пружины.
Другие вопросы по теме Физика
Популярные вопросы
- Скласти 5 речень що я роблю вдома по нимецькому...
3 - Das ist Taras. Er ist der Sohn von Andrij. Er ist Oxanas Sohn Das ist...
3 - Укажите, какое средство выразительности используется выражение дни......
3 - 10. Рассмотрите картину. В каком веке Москва могла выглядеть так? 1)...
2 - Правила оказания первой есле человека ударило током и он находится без...
3 - Задание 1. Вставьте буквы в окончания причастий, обоснуйте свой выбор...
3 - Решите уравнение: х*4 1/3=х...
3 - Скільки було олова, якщо при охолодженні на 800°С виділилося 828Дж теплоти?...
2 - Рассказ о том как ты был в гостях у людей бронзового века краткий рассказ...
3 - Область заданий \ Открытия и достижения Математика Медецына География...
2
T = 2π√(m/k)
где T - период колебаний, m - масса груза, k - жесткость пружины.
На графике представлены зависимости силы, действующей на груз, от его смещения от положения равновесия. Мы знаем, что сила, действующая на груз, связана со смещением по закону Гука:
F = kx
где F - сила, k - жесткость пружины, x - смещение от положения равновесия.
Из графика мы видим, что сила и смещение линейно связаны между собой. Значит, у нас есть линейная зависимость, что означает, что коэффициент наклона прямой на графике будет равен жесткости пружины k.
Давайте определим коэффициент наклона прямой, используя две точки на графике. Возьмем точки (0, 0) и (0.06, 0.3) и используем формулу:
k = (F2 - F1) / (x2 - x1)
где F1 и F2 - значения силы на графике, соответствующие значениям x1 и x2.
Подставим значения:
F1 = 0
F2 = 0.3 Н (прочитанное значение на оси силы)
x1 = 0 м
x2 = 0.06 м (прочитанное значение на оси смещения)
k = (0.3 - 0) / (0.06 - 0) = 0.3 Н/м
Таким образом, жесткость пружины равна 0.3 Н/м.