Где ошибка рассуждений? перемещение тела при прямолинейном равноускоренном движении без начальной скорости. закономерность звучит: перемещения, совершенные телом за каждую последующую секунду, будут относиться как нечетные числа: 1: 3: 5: 7. если ускорение будет 4 м/с^2, то за четвертую секунду по формуле a(t^2) *(2n-1) / 2= 14 м. (четное число, что противоречит). если ускорение будет 3 м/с^2, то за четвертую секунду по формуле a(t^2) *(2n-1) / 2= 10.5 м. (нечетного числа нет). так-же оно противоречит и второй закономерности: пропорциональность пути квадрату времени. так как полное расстояние за четыре секунд с ускорением 4 м/с^2 будет не 16 м, а 32 м.

Никакой ошибки нет, вы неверно поняли закономерность.

Пусть ускорение равно 4 м/с^2, тогда по формуле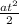 получим 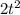(подставили значение ускорения).

Подставляем одну, две и три секунды и получаем результат 2м - 8м - 18м - 32м.

Теперь читаем еще раз закономерность: перемещения, совершенные телом за КАЖДУЮ ПОСЛЕДУЮЩУЮ секунду, а НЕ за все время движения. Т.е. наша формула считает общее перемещение, в то время как нам нужно лишь перемещение за каждую последующую секунду. Поэтому отнимаем путь, пройденный в предыдущую секунду, из общего пройденного пути на данный момент, чтобы найти перемещение в настоящую секунду. Получим 2м - 6м - 10м - 14м. Сократим на 2 и получим заданное соотношение 1м - 3м - 5м - 7м.