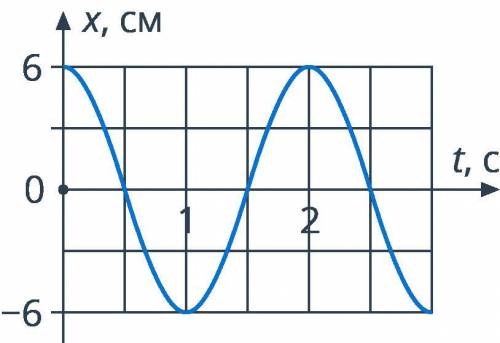
Физика решить ) На рисунке приведён график зависимости x(t) для гармонического колебания. Найдите амплитуду, частоту и период колебания. Запишите формулу зависимости x(t). Сколько колебаний произойдёт за 16 секунд?

Для решения данной задачи сначала определим амплитуду колебания, частоту и период колебания по графику зависимости x(t).

1. Амплитуда (A) колебания - это самое большое значение, которое принимает зависимость x(t) от времени t. В данном случае, амплитуда равна 2,5 см, так как это максимальное значение y на графике (положительное значение волны) и отсчеты по оси y начинаются с нуля. Поэтому амплитуда колебания равна 2,5 см.

2. Частота (f) колебания - это количество полных колебаний, которые совершает система за одну единицу времени. Можно определить частоту по формуле: f = 1 / T, где T - период колебания.

3. Период колебания (T) - это время, за которое система совершает одно полное колебание.

Давайте определим период колебания:
- Посмотрим на график и заметим, что система совершает полное колебание с 0 до А и обратно от А до 0. Это происходит за время t1 = 2с.
- Затем система снова совершает полное колебание от 0 до А и обратно от А до 0. Это происходит за время t2 = 2с.
- Таким образом, полное колебание совершается за время T = t1 + t2 = 4с.
- Получаем, что период колебания T равен 4 секундам.

Используя полученные значения амплитуды (2,5 см) и периода (4 сек), можем определить частоту колебания:
- f = 1 / T = 1 / 4 = 0,25 Гц.
- Частота колебания составляет 0,25 Гц.

Формула зависимости x(t) для гармонического колебания имеет вид: x(t) = A * cos(2πft + φ), где A - амплитуда, f - частота, t - время, φ - начальная фаза.

Найдем количество колебаний за 16 секунд:
- Зная период колебания T (4 сек), можем использовать формулу количества колебаний N = t / T, где t - заданный интервал времени.
- N = 16 / 4 = 4.
- За 16 секунд произойдет 4 колебания.

Таким образом, ответ на задачу:

Амплитуда колебания: 2,5 см
Частота колебания: 0,25 Гц
Период колебания: 4 секунды
Формула зависимости x(t): x(t) = 2,5 * cos(2π * 0,25t + φ)
Количество колебаний за 16 секунд: 4 колебания.