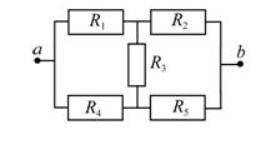
Физика Определите в цепи, представленной на рисунке, сопротивление Rab между точками а и b, если R1 = R5 = 10 Ом, а R2 = R3 = R4 = 5 Ом. (При решении используйте симметрию ветвей около точек а и b, принимая во внимание заданные значения сопротивлений).
ответ: Rab = 7 Ом.
Другие вопросы по теме Физика
Популярные вопросы
- Какой самый знаменитый зверь приокско-террасного заповедника?...
1 - Уникальные характеристики покрытосеменных является наличие...
3 - Найти крылатые выражения в повicтi мiсце для дракона...
2 - Значение лишайников в жизни растений...
2 - Найдите значение выражения: (0,7) во 2 степени...
3 - 5+5+5-5-5-5-5-5-5-5-555-5-5--5-5-55-9...
1 - Эволюция органов дыхания хордовых животных. (максимально коротко...
1 - Написать в тонкую тетрадь праздники иудаизма и христианства....
3 - Представьте число 8 5/12 в виде неправильной дроби...
3 - Свыводом , на тему : репродуктивной здоровье...
2
Давайте разделим данную цепь на две части, сосредоточив свое внимание на точках a и b. Посмотрим на треугольник, образованный резисторами R2, R3 и R4. Заметим, что эти резисторы соединены параллельно между собой. Поэтому мы можем заменить этот треугольник эквивалентным резистором сопротивлением R23 (обозначим его так), которое мы должны найти.
Используя формулу для сопротивления параллельного соединения, мы можем выразить R23:
1/R23 = 1/R2 + 1/R3 + 1/R4
Подставляем значения сопротивлений:
1/R23 = 1/5 + 1/5 + 1/5
1/R23 = 3/5
R23 = 5/3 Ом
Теперь можем заметить, что R1 и R5 соединены в параллель. Заменим их эквивалентным сопротивлением R15:
1/R15 = 1/R1 + 1/R5
1/R15 = 1/10 + 1/10
1/R15 = 2/10
R15 = 10/2 Ом
R15 = 5 Ом
Мы получили два эквивалентных резистора: R23 = 5/3 Ом и R15 = 5 Ом. Эти два резистора соединены последовательно между точками a и b.
Чтобы найти общее сопротивление между точками a и b, сложим сопротивления R23 и R15:
Rab = R23 + R15
Rab = 5/3 + 5
Rab = (5+15)/3
Rab = 20/3 Ом
Последний шаг - упростить результирующую дробь:
Rab = (20/3 * 3/3) / 3
Rab = 20/9 Ом
Итак, сопротивление Rab между точками a и b равно 20/9 Ом, что можно приближенно записать как 2.2 Ом.