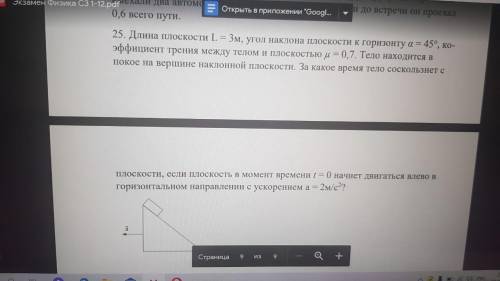
Физика Длина плоскости L=3м угол наклона плоскости к горизонту альфа=45градусов, коэффициент трения между телом и плоскостью м=0.7, тело находиться в покое на вершине наклонной плоскости. За какое время тело соскользнёт с плоскости, если плоскость в момент времени t=0 начнёт двигаться влево в горизонтальном направлении с ускорением а=2м/с^2

Для решения данной задачи, мы можем разделить ее на две части: движение плоскости и движение тела.

1. Рассмотрим движение плоскости:
У нас есть начальное ускорение плоскости a=2 м/с^2 и начальная скорость плоскости v=0 м/с. Мы хотим найти время, через которое плоскость сдвинется на длину L=3 м.

Мы знаем, что сдвижение плоскости задается уравнением:
L = v*t + (1/2)*a*t^2

Подставим известные значения:
3 = 0*t + (1/2)*2*t^2

Упростим уравнение:
3 = t^2

Возьмем корень из обеих частей:
t = √3
t ≈ 1.73 секунды

Таким образом, плоскость сдвинется на длину L=3 м за примерно 1.73 секунды.

2. Рассмотрим движение тела:
У нас есть угол наклона плоскости α=45 градусов и коэффициент трения между телом и плоскостью μ=0.7. Тело находится в покое на вершине наклонной плоскости. Мы хотим найти время, через которое тело соскользнет с плоскости.

Сначала найдем компоненты силы трения и веса, действующие на тело:
F_параллель = m*g*sin(α)
F_перпендикулярно = m*g*cos(α)

где m - масса тела, g - ускорение свободного падения, α - угол наклона плоскости.

F_параллель = m*g*sin(45) = m*g*(√2/2) ≈ 0.7*m*g
F_перпендикулярно = m*g*cos(45) = m*g*(√2/2) ≈ 0.7*m*g

Сила трения F_трения можно найти, используя формулу:
F_трения = μ * F_перпендикулярно

F_трения = 0.7 * (0.7 * m * g) ≈ 0.49*m*g

Так как плоскость начала двигаться в момент времени t=0, то тело будет оставаться на покоящейся плоскости до тех пор, пока сила трения не превысит предельное значение. То есть:

F_трения = F_параллель

0.49*m*g = 0.7*m*g * (√2/2)

0.49 = 0.7 * (√2/2)

Теперь найдем время t, через которое тело начнет двигаться:
t = √(2*L / (g * sin(45)))

Подставим известные значения:
t = √(2*3 / (9.8 * (√2/2)))

Упростим выражение:
t = √(6 / (9.8 * (√2/2)))

t = √(6 / (9.8 / √2))

t = √(6 * √2 / 9.8)

t ≈ √(12/9.8) ≈ √(1.22)

t ≈ 1.10 секунды

Таким образом, тело начнет соскользывать с плоскости примерно через 1.10 секунды.