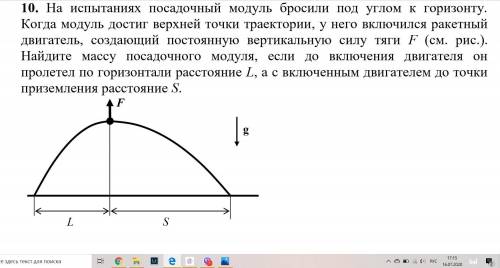
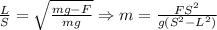Физика 9 класс, механика решить задачу по данному разделу. Сам никак не могу додуматься как связать движение тела, брошенного под углом к горизонту, к которому потом прикладывают СИЛУ. Задача серьёзная, но и даю много. Буду очень благодарен за грамотное решение, но сильно подробное тоже не требуется ;)

Физика 9 класс, механика решить задачу по данному разделу. Сам никак не могу додумать

Ответы

андрев1 15.10.2020 15:23

$m=\frac{F}{g-\frac{L^2g}{S^2} }$

Объяснение:

До включения ракетного двигателя модуль двигался как обычное тело, брошенное под углом к горизонту, расстояние от точки броска до наивысшей точки траектории определяется формулой

$L=\frac{v_0^2sin2\alpha }{2g}$ (1)

После включения двигателя, ускорение свободного падения уменьшилось на величину равную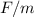 F/m и стало составлять

$g'=g-\frac{F}{m}$ (2)

Следовательно, новая дальность уже высчитывается для тела, брошенного горизонтально

$S=v_0cos\alpha \sqrt{\frac{2h}{g-\frac{F}{m} } }$ (3)

Высоту полета h можно найти по формуле

$h=\frac{v_0^2sin^2\alpha }{2g}$ (4)

Подставляя (4) в (3) и выполняя все преобразования, получим

$S=\frac{v_0^2sin2\alpha }{2} \sqrt{\frac{1}{g(g-\frac{F}{m} )} }$

С учетом того, что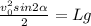 $\frac{v_0^2sin2\alpha}{2} =Lg$ это следует из формулы (1)

$S=\sqrt{\frac{L^2g^2}{g(g-\frac{F}{m} )} }$

Или

$S^2=\frac{L^2g^2}{g^2-g\frac{F}{m} } = m=\frac{F}{g-\frac{L^2g}{S^2} }$ .

ПОКАЗАТЬ ОТВЕТЫ

Zigmynda11 15.10.2020 15:23

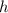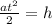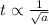Рассмотрим падение тела с некоторой постоянной высоты . Понятно, что время падения зависит только от ускорения, приложенного к телу и начального значения вертикальной компоненты скорости, вне зависимости от горизонтальной составляющей. Поэтому из формулы $\frac{at^2}{2}=h$ становится ясно, что $t\propto \frac{1}{\sqrt{a}}$ .

Все силы направлены вертикально, а значит, горизонтальная компонента скорости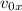 $v_{0x}$ сохраняется. Поэтому 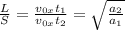$\frac{L}{S}=\frac{v_{0x}t_{1}}{v_{0x}t_{2}}=\sqrt{\frac{a_{2}}{a_{1}} }$ . При этом 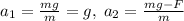$a_{1}=\frac{mg}{m}=g,\; a_{2}=\frac{mg-F}{m}$ . Имеем: $\frac{L}{S}=\sqrt{\frac{mg-F}{mg} } \Rightarrow m=\frac{FS^2}{g(S^2-L^2)}$