ФИЗИКА 10 КЛАСС, МЕХАНИКА, ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ Маленькая шайба соскальзывает с некоторой высоты h по гладкой наклонной плоскости, плавно переходящей на горизонтальный участок гладкой поверхности, и испытывает центральное абсолютно упругое соударение с шайбой вдвое меньшей массы. Вторая шайба после соударения попадает на наклонную шероховатую поверхность, плавно сопряжённую с горизонтальной поверхностью посредством гладкого участка. Определите угол α, который образует с горизонтом шероховатая наклонная поверхность, если эта шайба поднимается по ней на такую же высоту h. Коэффициент трения между шайбой и шероховатой поверхностью равен μ = 0.26.
Я немного расписал задачу на второй картинке(возможно неправильно), но не знаю, что делать дальше

Другие вопросы по теме Физика
Популярные вопросы
- Начерти схему состава ученического стола (рабочего стола)...
2 - Встречаются ли скелеты у простейших? какие они выполняют функции?...
3 - M0,8т v 0,6м3 p ? как решить мне надо...
1 - Назовите особенности строения наружного скелета моллюсков...
1 - Трамвай ехал на север,резко повернул на восток,в каком направлении...
3 - Напишите интересные факты о тютчеве можно быстрей я на уроке...
1 - Объясните как это решается - 5(x-3y)-0,5(7x+4y)-4,5x...
2 - Сторона основания правильной четырех угольной призмы равна 8 см. диагональ...
1 - Перевести в обыкновенную дробь 1,21 (8)...
3 - Нужно составить текст по теме томирис про батыра 40 50 слов...
3
Угол наклона равен 8.3 градуса
Объяснение:
Данная задача является первой задачей в олимпиаде "Ломоносов" 2021-2022 по физике 10-11 класс и будет решена в общем виде, так как у всех были разные значения коэффициента трения:
Анимацию столкновения можно глянуть тут: https://youtu.be/yDroGp3K5Q0
На высоте h первая шайба обладала потенциально энергией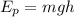 , которая затем перешла целиком в энергию кинетическую тела, когда оно скатилось
, которая затем перешла целиком в энергию кинетическую тела, когда оно скатилось 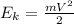
Так как поверхность гладкая и потерь энергии не было, то:
Пусть U1 - скорость первой шайбы после столкновения, а U2 - скорость второй, тогда запишем закон сохранения импульсов:
Так как удар абсолютно упругий запишем сохранение кинетических энергий
Имея систему
Найдем значение U2:
Подставим в уравнение импульсов:
Когда меньшее тело выходит на шероховатую наклонную плоскость то на него действуют силы, что указаны на рисунке 5, отсюда:
Из наклонной плоскости где один катет против угла альфа равен H, а гипотенуза равна S, выразим S:
Согласно формуле: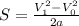 , где V0 - U2, а V1 равно нулю, так как конечная скорость равна нулю, подставим:
, где V0 - U2, а V1 равно нулю, так как конечная скорость равна нулю, подставим: