Электростатика. нужна . ( все свои 66 )
в приоретете решение 13, 10 и 9 . но еще с остальными номерами начиная от 4ого. т.к я крайне сомневаюсь в своем решении. заранее больше)
Другие вопросы по теме Физика
Популярные вопросы
- Определи количество ячеек в диапазоне B1:B12....
2 - Возможно ли увеличение скорости автомобиля при работе его двигателя...
3 - Подвір я складається з п яти рівних квадратів. Визнач площу подвір...
2 - ЛЮЮДИ Проверьте через 10 минут сдавать! H E L P...
1 - Составь словесную модель по математической. x−y=28 xy=15 ответ:...
1 - Как решить задачу: Объем потребления задан формулой С = 700 + 36...
3 - При паралельному перенесенні точка А(1;3) переходить у точку В(-1;4)....
2 - Aufgabe 2: fülle die Lücken richtig aus / заполни правильно пропуски...
3 - Написати переказ з елементами роздуму за текстом Закопане золото...
3 - Найдите все значение переменноё при которых квадратный трехчлен-3x^2-x-12...
2
13)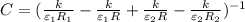
10)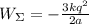
9) 1.843 мДж/м
Объяснение:
13. Поле в сферическом конденсаторе создаётся только зарядами внутренней обкладки, а в диэлектриках – ещё и связанным зарядом.
Для определённости, пусть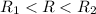 ,
,
10. Энергия взаимодействия левого заряда с центральным: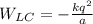 ;
;
энергия взаимодействия правого заряда с центральным: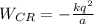 ;
;
энергия взаимодействия левого заряда с правым: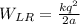 ;
;
Полная энергия взимодействия: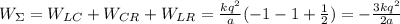 ;
;
9. Из Теоремы Гаусса, поле бесконечной струны может быть вычислено, как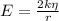 , где
, где 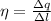 – линейное распределение заряда по струне, удельное к длине.
– линейное распределение заряда по струне, удельное к длине.
В любой электростатической системе потенциал представляется функцией, противоположной к первообразной напряжённости поля, а значит, для бесконечной струны потенциал может быть вычислен, как: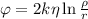 , где
, где 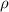 – радиус нулевого потенциала, который выбирается свободно (но не меняется в ходе решения задачи), и чаще всего за радиус
– радиус нулевого потенциала, который выбирается свободно (но не меняется в ходе решения задачи), и чаще всего за радиус 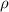 нулевого потенциала уднобно принять радиус струны.
нулевого потенциала уднобно принять радиус струны.
Потенциальная энергия взаимодействия куска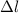 второй струны, находящейся на расстоянии
второй струны, находящейся на расстоянии 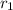 от первой
от первой 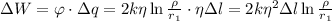 .
.
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии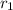 , удельная к длине:
, удельная к длине: 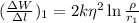 .
.
Потенциальная энергия взаимодействия второй струны, находящейся от первой на расстоянии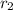 , удельная к длине:
, удельная к длине: 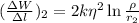 .
.
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от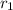 до
до 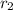 равна разности потенциальных энергий этих конфигураций, удельных к длине:
равна разности потенциальных энергий этих конфигураций, удельных к длине:
Работа, удельная к длине, совершаемая полем при увеличении расстояния между струнами от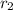 до
до 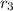 будет равна:
будет равна: 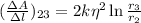 ;
;
Учитывая, что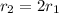 ,
,
и, кроме того, поскольку: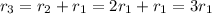 , то:
, то:
Стало быть:
Отсюда: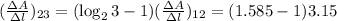 мДж/м
мДж/м 
= 1.843 мДж/м .