1. Физика
  2. Две пружины, жесткостью k1

Две пружины, жесткостью k1 = 10 Н/м и k2 = 2,5 Н/м, соединены последовательно. Пружины растянули за свободные концы в разные стороны, совершив работу 10 мДж. Какова деформация первой пружины? ответ приведите в см.

buchelnikova84 buchelnikova84    1   06.08.2020 11:22    5

Ответы
veratokareva31 veratokareva31  15.10.2020 15:46

2cm

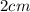
Объяснение:

Проще решить эту задачу с законов сохранения, в частности законом сохранения энергии, тогда получается:

E2 - E1 = зA

\frac{k1зx1^{2} }{2} + \frac{k2зx2^2}{2} = F(зx2 - зx1)

k1зx1^2 + k2зx2^2 = 2F(зx2 - зx1)

Воспользуемся, тем что систему пружин растягивают в разные стороны с одинаковыми силами, будем считать на время действия этих сил деформации упругими, тогда:

F1 = F\\F2 = F

F1 = k1зx1\\F2 = k2зx2\\k1зx1 = k2зx2

зx1 = \frac{k2}{k1}зx2

Также известно, что:

F(зx2 - зx1) = A

k1зx1^2 + k2зx2^2 = 2A

k1(\frac{k2}{k1}зx2)^2 + k2зx2^2 = 2A

\frac{k2^{2} }{k1}зx2^2 + k2зx2^2 = 2A

зx2^2 = \frac{2A}{(\frac{k2^2}{k1} + k2)}

зx2 = \sqrt{\frac{2A}{(\frac{k2^2}{k1} + k2)} }

k1зx1 = k2зx2

k1зx1 = k2\sqrt{\frac{2A}{\frac{k2^{2} }{k1} + k2 } }

зx1 = \frac{k2\sqrt{\frac{2A}{\frac{k2^2}{k1} + k2 } } }{k1}

зx1 = 0,02 m ⇔ 2cm

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
MashaBelous MashaBelous  30.04.2020 08:54
с физикой Найдите информацию о том, какую роль сыграл Александр Григорьевич Столетов в исследовании явления фотоэффекта. Почему, с вашей точки зрения, он не получил Нобелевскую...
назым24 назым24  30.04.2020 08:54
Присвой данным веществам порядковый номер 1, 2 или 3 в зависимости от их свойств теплопроводности, начиная с наименьшей. ​...
VladIslaV231678 VladIslaV231678  30.04.2020 08:53
Имеем стакан холодной воды, стакан кипятка, раскаленный металлический гвоздь. В одном случае гвоздь опускают в холодную воду, в другом в горячую. В каком случае гвоздь...
murrrКотя murrrКотя  07.04.2021 18:53
Расчет интерференционной картины от двух источников​...
Raud1 Raud1  07.04.2021 18:53
На дифракційну решітку, яка має 100 штрихів на 1мм, падає нормально світло довжиною хвилі 500нм. Визначти кути дифракції, під якими розміщені максимуми першого і третього...
iraapukhtina7 iraapukhtina7  07.04.2021 18:53
Определить высоту здание и количество этажей есле барометр на 1 этаже показывает 767 мм рт ст, а на последнем этаже 748 мм рт ст. Высота одного этажа 2.7 м...
Ангелина0113 Ангелина0113  07.04.2021 18:52
Определить высоту дерева, если длина отбрасываемой им тени равна 28м, а длина тени человека, стоящего параллельно дереву 21м. Рост человека 1,5м....
popoposa popoposa  07.04.2021 18:51
Лабораторная работа. Определение показателя преломления стекла. 1.Положить поперек полоски света стеклянную пластину. 2. Прочертить карандашом на бумаге линии вдоль преломляющих...
Brakorenko88 Brakorenko88  07.12.2020 09:31
Прямоугольный открытый резервуар с размерами дна 3 х 5 м предназначен для хранения 30 м3 воды. Определить силы давления на стенки и дно резервуара....
НастЮхАforever НастЮхАforever  07.12.2020 09:29
4. Укажите определение следующих терминов А) Плавление - это Б) Кипение – это...

Популярные вопросы