Две материальные точки движутся по одной прямой, совпадающей с осью 0x декартовой системы координат. Закон движения первой точки имеет вид 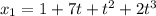 , а ускорение второй точки изменяется согласно уравнению
, а ускорение второй точки изменяется согласно уравнению 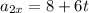 . В начальный момент времени вторая точка имела координату
. В начальный момент времени вторая точка имела координату 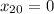 и скорость
и скорость 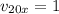
Другие вопросы по теме Физика
Популярные вопросы
- Значение литературы для людей 21 века эссе...
1 - Укажіть структури які можуть мати лише клітини тварин а)щільна клітинна оболонка...
3 - Впервые идея о шарообразности была видвинута в ____веке до н.э. древне-греческими...
3 - Оцініть значення екологічних досліджень на сучасному етапі розвитку людства...
1 - Дано: L1=17м g≈10H/м L2=12м V-?...
3 - Обратная функция y³=1-x³+ график ...
1 - вас надо составить предложенияи вместо круглишочков букв и запятых написать...
3 - фишбоун почему мальчик остался один мне нужен проблема,пичины,вывод,факты аргументы...
1 - Жаратылыстың у ғылымдарының зерттеу нысанын сәйкестендіру алады. жаралыстану...
1 - назовите один факт из истории вашего региона благодаря которому ваш регион стал...
1
В момент времени t = 1 с ускорения точек были одинаковы, относительная скорость точек v₂₋₁ = 3 м/с, точки находились на расстоянии 5 м друг от друга
Объяснение:
При движении координата 1-й точки изменяется по закону
x₁(t) = 1 + 7t + t² + 2t³
Скорость движения 1-й точки
v₁(t) = x' = 7 + 2t + 6t²
Ускорение движения 1-й точки
a₁(t) = v₁'(t) = 2 + 12t
Ускорение движения 2-й точки задано
a₂(t) = 8 + 6t
Момент времени t, в который ускорения точек одинаковы, определим из уравнения
2 + 12t = 8 + 6t
6t = 6
t = 1 (с)
Cкорость движения 2-й точки
v₂(t) =v₂₀ + ∫a₂(t) dt = 1 + ∫(8 + 6t) dt = 1 + 8t +3t²
В моvент времени t = 1 скорости точек
v₂(1) = 1 + 8 + 3 = 12 (м/с)
v₁(t) = 7 + 2 + 6 = 15 (м/с)
Относительная скорость
v₂₋₁ = v₁(t) - v₂(1) = 15 - 12 = 3 (м/с)
Координата 2-й точки
х₂(е) = х₂₀ + ∫v₂(t) d = ∫(1 + 8t + 3t²) dt = t + 4t² + t³
В моvент времени t = 1 координаты точек
x₁(1) = 1 + 7 + 1 + 2 = 11 (м)
х₂(1) = 1 + 4 + 1 = 6 (м)
Точки находились друг от друга на расстоянии
s₁₋₂ = 11 - 6 = 5 (м)