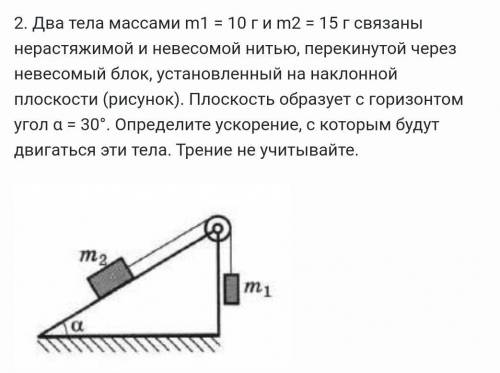
Два тела массами m1 = 10 г и m2 = 15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (рисунок). Плоскость образует с горизонтом угол α = 30°. Определите ускорение, с которым будут двигаться эти тела. Трение не учитывайте
Другие вопросы по теме Физика
Популярные вопросы
- Abcd - параллелограмм. найдите координаты точки d, если a(-4; 3),b(5;...
1 - От числа 70 отняли сумму двух восьмёрок и получили...
3 - Уведомления что для тебя значит в жизни ваша мать...
3 - Походы в театры музеи на выставки в кино концертные залы -развечениеили...
2 - Аргумент для сочинения проблемного характера проблема : судьба человека...
1 - Написать 5 сложно подчиненных предложений с придаточным определением,...
3 - Решить завтро контрольная 1.)одна из сторон прямоугольника ровна 7...
3 - Интеграл от 0 до 1 от dx/1+x^2 1 s dx/1+x^2 0...
2 - Решите уравнение √2*sin(x/4-x/52) + sin(x/52) = -1...
2 - Слова эмоции какими словами можно описать милодию грусная или весёлая...
3
1. Разложение силы тяжести:
- Сила тяжести F1, действующая на тело массой m1, можно разложить на две составляющие:
- F₁₁ - перпендикулярную к плоскости наклона, направленную вниз
- F₁₂ - параллельную плоскости наклона влево
- Сила тяжести F2, действующая на тело массой m2, можно также разложить на две составляющие:
- F₂₁ - перпендикулярную к плоскости наклона, направленную вниз
- F₂₂ - параллельную плоскости наклона вправо
2. Силы, действующие на каждое тело:
- На тело m1 действуют:
- F₁₁ - перпендикулярная сила, направленная вниз
- Fтр₁ - сила трения, направленная вверх
- T - натяжение нити, направленное слева
- На тело m2 действуют:
- F₂₁ - перпендикулярная сила, направленная вниз
- Fтр₂ - сила трения, направленная вправо
- T - натяжение нити, направленное справа
3. Запишем уравнения второго закона Ньютона для каждого из тел:
- Для тела m1: Fг₁ - Fтр₁ - T = m₁ * a
- Fг₁ = m₁ * g * sin(α)
- Fтр₁ = μ₁ * m₁ * g * cos(α)
- Для тела m2: Fг₂ - Fтр₂ + T = m₂ * a
- Fг₂ = m₂ * g * sin(α)
- Fтр₂ = μ₂ * m₂ * g * cos(α)
где μ₁ и μ₂ - коэффициенты трения между телами и плоскостью наклона и определяются данными условиями задачи (если не указано, то можно считать их равными нулю).
4. Найдем значение ускорения (а):
- Из уравнения для тела m1: Fг₁ - Fтр₁ - T = m₁ * a
- Из уравнения для тела m2: Fг₂ - Fтр₂ + T = m₂ * a
- Подставим значения из шага 3:
- m₁ * g * sin(α) - μ₁ * m₁ * g * cos(α) - T = m₁ * a
- m₂ * g * sin(α) - μ₂ * m₂ * g * cos(α) + T = m₂ * a
- Cложим оба уравнения:
- m₁ * g * sin(α) - μ₁ * m₁ * g * cos(α) - T + m₂ * g * sin(α) - μ₂ * m₂ * g * cos(α) + T = m₁ * a + m₂ * a
- Упростим:
- g * (m₁ * sin(α) + m₂ * sin(α)) - g * (μ₁ * m₁ * cos(α) + μ₂ * m₂ * cos(α)) = (m₁ + m₂) * a
- Делим обе части уравнения на (m₁ + m₂):
- g * sin(α) - (μ₁ * m₁ * cos(α) + μ₂ * m₂ * cos(α)) = a
- Упрощаем выражение:
- a = g * (sin(α) - (μ₁ * m₁ * cos(α) + μ₂ * m₂ * cos(α))/(m₁ + m₂))
5. Подставляем значения из условия задачи и вычисляем ускорение:
- g = 9.8 м/с² (ускорение свободного падения)
- α = 30°
- μ₁ = μ₂ = 0 (если не указаны иная)
- Подставляем значения:
- a = 9.8 * (sin(30°) - (0 * 10 * cos(30°) + 0 * 15 * cos(30°))/(10 + 15))
- a = 9.8 * (0.5 - 0) = 4.9 м/с²
Ответ: Ускорение, с которым будут двигаться эти тела, составляет 4.9 м/с².