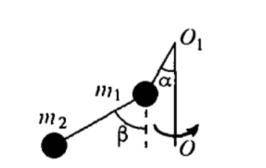
Два небольших по размерам шарика связаны нитью и прикреплены к оси OO1 другой нитью в √3 раз меньшей длины. Система вращается с постоянной угловой скоростью вокруг вертикальной оси OO1 (см. рис.). Нити составляют углы alpha =30° и beta =60° с вертикалью. Найдите отношение масс m1/m2 шариков.

Для решения данной задачи, нам понадобятся некоторые физические законы, в частности, законы сохранения момента импульса и силы тяжести.

Введем обозначения:
m1 - масса первого шарика
m2 - масса второго шарика
l1 - длина нити, соединяющей первый шарик с осью OO1
l2 - длина нити, соединяющей второй шарик с осью OO1
ω - угловая скорость вращения системы
g - ускорение свободного падения (около 9.8 м/с^2)
α - угол между первой нитью и вертикалью
β - угол между второй нитью и вертикалью

Воспользуемся законом сохранения момента импульса:
m1*l1^2*ω + m2*l2^2*ω = Постоянная (1)

Также, на шарики действует сила тяжести, которая направлена компонентами по нитям. Поэтому, можно записать уравнение для силы по оси O1O:
m1*g*sin(α)*l1 - m2*g*sin(β)*l2 = 0 (2)

Из задания, известно, что l2 = l1/√3, α = 30° и β = 60°. Подставим эти значения в уравнение (2) и упростим его:
m1*g*sin(30°)*l1 - m2*g*sin(60°)*(l1/√3) = 0
(m1*0.5*l1) - (m2*0.866*l1/√3) = 0
0.5*m1*l1 - 0.5*m2*l1/√3 = 0
(m1 - m2/√3)*l1 = 0

Так как l1 не равно 0, то имеем:
m1 - m2/√3 = 0
m1 = m2/√3 (3)

Теперь, подставим выражение (3) в уравнение (1):
m1*l1^2*ω + m2*l2^2*ω = Постоянная
(m2/√3)*l1^2*ω + m2*(l1/√3)^2*ω = Постоянная
m2*ω*(l1^2/√3 + l1^2/3) = Постоянная
m2*ω*(4/3*l1^2/√3) = Постоянная
m2*ω*(4/3)*l1^2/√3 = Постоянная
m2*l1^2/√3 = Постоянная

Получаем, что m2*l1^2/√3 = Постоянная, что означает, что отношение масс шариков равно √3.
Таким образом, отношение масс m1/m2 шариков равно √3.