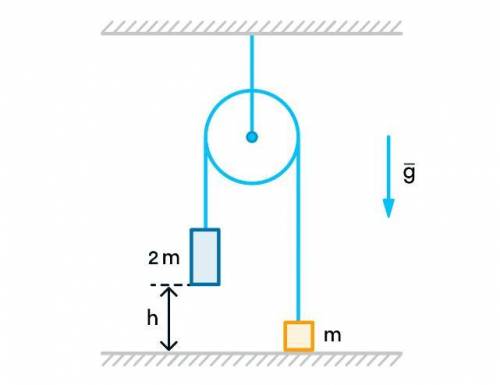
Два груза связаны невесомой нерастяжимой нитью ,перекинутой через легкий блок, прикрепленный к потолку. В начальный момент груз массой m удерживают на поверхности пола, а груз массой 2m находиться на высоте h=167 см от этой поверхности. Через какое время t груз массой 2m удариться о пол, после того как груз массой m опустят ? Трением в системе пренебречь. g=10 м/с2. ответ вырази в секундах и округли до целого числа

Для решения данной задачи мы можем использовать закон сохранения энергии.

В начальный момент груз массой m удерживается на полу, поэтому его потенциальная энергия равна нулю. Потенциальная энергия груза массой 2m, находящегося на высоте h, равна mgh, где g = 10 м/с^2 - ускорение свободного падения.

Когда груз массой m опускают, он начинает двигаться вниз и его потенциальная энергия уменьшается до нуля. При этом, его кинетическая энергия возрастает и становится равной масса m, умноженная на его скорость v.

Таким образом, уравнение сохранения энергии примет следующий вид:

mgh = 1/2 * m * v^2

Раскроем скобки:

2gh = v^2

Найдем значение скорости v:

v = sqrt(2gh)

После этого, мы можем применить второй закон Ньютона для груза массой 2m при его свободном падении:

F = 2mg = m * a

Где F - сила, действующая на груз массой 2m, m - его масса и a - его ускорение.

Учитывая, что а = dv/dt (где v - скорость груза массой 2m, t - время), получим:

2mg = 2m * dv/dt

Сократим на 2m:

g = dv/dt

Теперь мы можем выразить ускорение груза массой 2m через его скорость:

dv = g * dt

Выразим и интегрируем обе части уравнения:

∫(1/v) dv = ∫g dt

ln(v) = gt + C

где C - константа интегрирования.

Применим экспоненту к обеим частям уравнения:

v = exp(gt + C)

v = A * exp(gt)

где A - произвольная постоянная.

Теперь мы можем найти значение постоянной A, используя начальные условия задачи. В начальный момент времени, скорость груза массой 2m равна нулю (так как он удерживается на высоте). Поэтому:

v = 0 при t = 0

Используя это условие, найдем значение постоянной A:

0 = A * exp (g * 0)

0 = A

Получаем, что A = 0.

Теперь, найдем время t, через которое груз массой 2m ударится о пол. Для этого приравняем выражение для скорости v к нулю:

exp(gt) = 0

exp(gt) = exp(0)

gt = 0

t = 0 / g

t = 0 секунд.

Таким образом, груз массой 2m ударится о пол сразу же после того, как груз массой m опустят.

Ответ: t = 0 секунд.