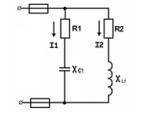
Для разветвленной цепи переменного тока при I1 = 5A, XLI = 6 Ом; ХС2 = 4 Ом; R1 = 3 Ом; R2= 8 Ом. Определить полное сопротивление цепи, токи в ветвях, ток цепи, активную мощность, реактивную и
полную мощности. Построить векторную диаграмму.

Для решения данной задачи сначала определим общее сопротивление цепи. Общее сопротивление цепи (Z) может быть найдено с использованием формулы Ohm's Law, где Z = √(R^2 + X^2).
Для нашей цепи R = R1 + R2 = 3 Ом + 8 Ом = 11 Ом и X = XL1 + XC2 = 6 Ом - 4 Ом = 2 Ом.
Подставляя значения в формулу, получаем Z = √(11^2 + 2^2) = √(121 + 4) = √125 = 11.18 Ом.

Теперь рассчитаем токи в ветвях. Используем формулу тока, где I = V/Z, где V - напряжение.
Перед тем, как рассчитать токи, нам нужно найти напряжение V, используя формулу напряжения для разветвленной цепи, где V = I1 * Z.
Подставляя значения, получаем V = 5 A * 11.18 Ом = 55.9 В.

Теперь мы можем рассчитать токи в ветвях.
Для ветви с индуктивным реактивным сопротивлением, используем формулу I1 = V / XLI, где XLI - индуктивное реактивное сопротивление.
Подставляя значения, получаем I1 = 55.9 В / 6 Ом = 9.32 A.

Для ветви с емкостным реактивным сопротивлением, используем формулу I2 = V / XC2, где XC2 - емкостное реактивное сопротивление.
Подставляя значения, получаем I2 = 55.9 В / 4 Ом = 13.98 A.

Теперь рассчитаем ток цепи, который равен сумме токов в ветвях, то есть I = I1 + I2 = 9.32 A + 13.98 A = 23.3 A.

Активная мощность (P) в цепи может быть найдена с использованием формулы P = I^2 * R.
Подставляя значения, получаем P = (23.3 A)^2 * 11 Ом = 6239.09 Вт.

Реактивная мощность (Q) может быть найдена с использованием формулы Q = I^2 * X.
Подставляя значения, получаем Q = (23.3 A)^2 * 2 Ом = 1079.38 ВАР (вары).

Полная мощность (S) может быть найдена с использованием формулы S = √(P^2 + Q^2).
Подставляя значения, получаем S = √(6239.09 Вт^2 + 1079.38 ВАР^2) = √(38875484.08 Вт^2 + 1165986.88 ВАР^2) = √(40041471.96) = 6325.14 ВА.

Таким образом, полное сопротивление цепи составляет 11.18 Ом, токи в ветвях равны 9.32 A и 13.98 A соответственно, ток в цепи составляет 23.3 A, активная мощность составляет 6239.09 Вт, реактивная мощность составляет 1079.38 ВАР, а полная мощность составляет 6325.14 ВА.

Чтобы построить векторную диаграмму, мы используем комплексные числа, где векторное представление активного сопротивления - действительная часть комплексного сопротивления, а реактивного сопротивления - мнимая часть комплексного сопротивления.
Общее сопротивление цепи Z может быть представлено в виде комплексного числа Z = R + jX, где j - мнимая единица.
Для нашей цепи Z = 11.18 + j2 Ом.
Токи в ветвях можно представить в виде комплексных чисел I1 = I1 + j0 и I2 = I2 - j0, где I1 и I2 - скаляры, а j0 - исключенная мнимая часть тока.
Ток цепи I = I1 + I2 = (I1 + j0) + (I2 - j0) = I1 + I2.
На векторной диаграмме вектор тока в ветви с индуктивным реактивным сопротивлением будет находиться над действительной осью, а ветви с емкостным реактивным сопротивлением - ниже действительной оси. Векторы I1 и I2 будут добавлены для получения вектора I.

Надеюсь, это решение понятно. Если у вас есть какие-либо вопросы, пожалуйста, дайте мне знать.