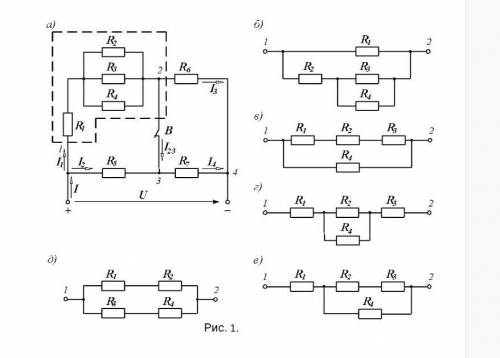
Для электрической цепи постоянного тока (рис. 1.7 с. 16) определить общий ток I, токи I1, I2, I3, I4 в ветвях резисторов и ток I23 в перемычке 2 – 3 цепи при разомкнутом и замкнутом выключателе В, а также напряжение U23 между узлами 2 и 3 при разомкнутом выключателе. Напряжение U, подводимое к электрической цепи, сопротивления резисторов R1 – R7, положение выключателя В и участок электрической цепи между узлами 1 и 2 цепи, показанный на рис. 1.7 пунктиром для соответствующего варианта рис. 1.7 б – е, приведены в таблице 1.2(с. 17). Примечание. В вариантах 31 – 60 сопротивление резистора R2=0. Сделать проверку решения, используя I закон Кирхгофа и уравнение баланса мощностей.

Для решения этой задачи по началу нужно разобраться с терминами и основными законами, применяемыми в электрических цепях.

Закон Кирхгофа - это основной закон, который гласит, что сумма токов, втекающих в узел, равна сумме токов, идущих из этого узла.

Обозначения:
- I1, I2, I3, I4 - токи в различных ветвях цепи,
- I23 - ток в перемычке 2-3 цепи,
- U23 - напряжение между узлами 2 и 3,
- U - напряжение, подводимое к электрической цепи,
- R1-R7 - сопротивления резисторов.

Шаг 1:
Посмотрим на рисунок и найдем все величины, известные нам из таблицы 1.2 (с. 17). В данном случае из таблицы нам дано, что напряжение U=4 В и R2=0.

Шаг 2:
Начнем с решения задачи при разомкнутом выключателе В. В этом случае, ток будет проходить только через резистор R1 и перемычка 1-2 цепи будет замкнута. Сопротивление R2=0, поэтому он фактически не будет препятствовать движению тока. Тогда общий ток I будет равен току I1, а I23 = 0, так как перемычка 2-3 разомкнута.

Шаг 3:
Так как резистор R1 соединен последовательно с источником напряжения U, то применяем формулу для сопротивления резисторов, соединенных последовательно:
R_экв = R1 = 10 Ом

Затем, используя закон Ома (U = I * R), найдем ток I1:
U = I1 * R_экв => I1 = U / R_экв = 4 В / 10 Ом = 0.4 А

Шаг 4:
Теперь рассмотрим случай, когда выключатель В замкнут. В этом случае, ток будет проходить через все резисторы, включая перемычку 2-3 цепи. Итак, чтобы найти общий ток I, сначала найдем сопротивление эквивалентной цепи. Так как резистор R2=0, он не оказывает сопротивление и будет обходиться током. Итак, сопротивление эквивалентной цепи равно:
1 / R_экв = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4 + 1 / R5 + 1 / R6 + 1 / R7
1 / R_экв = 1 / 10 + 1 / 0 + 1 / 20 + 1 / 20 + 1 / 30 + 1 / 10 + 1 / 30
1 / R_экв = 0.1 + 0 + 0.05 + 0.05 + 0.033 + 0.1 + 0.033
1 / R_экв = 0.366
R_экв = 1 / 0.366 = 2.732 Ом

Шаг 5:
Теперь, используя закон Ома (U = I * R), найдем общий ток I:
U = I * R_экв => I = U / R_экв = 4 В / 2.732 Ом = 1.464 А

Шаг 6:
Так как ток I проходит через все резисторы, для определения токов I1, I2, I3, I4 применяем закон Кирхгофа. Сумма токов, втекающих в узел 2, равна сумме токов, идущих из этого узла:
I2 - I1 + I23 = 0
I2 = I1 - I23

Шаг 7:
Подставляем найденные значения в данное уравнение:
I2 = 0.4 А - I23

Шаг 8:
Теперь, чтобы найти ток I23, рассмотрим цепь, включающую только перемычку 2-3. В этой цепи I23 будет равен общему току I, так как выключатель В замкнут и ток I будет проходить через всю цепь. Таким образом:
I23 = I = 1.464 А

Шаг 9:
Наконец, чтобы найти U23, найдем разность потенциалов между узлами 2 и 3, используя закон Ома:
U23 = I23 * R3 = 1.464 А * 20 Ом = 29.28 В

Проверка решения:
Мы можем проверить наше решение, применяя закон Кирхгофа и уравнение баланса мощностей. Закон Кирхгофа уже использовался при определении токов I1, I2, I3, I4 и I23. Уравнение баланса мощностей гласит, что сумма мощностей, потерянных в сопротивлениях, равна мощности источника напряжения:
P_источника = P1 + P2 + P3 + P4 + P5 + P6 + P7
P_источника = U * I
P1 = I1^2 * R1
P2 = I2^2 * R2
P3 = I3^2 * R3
P4 = I4^2 * R4
P5 = I5^2 * R5
P6 = I6^2 * R6
P7 = I7^2 * R7

Подставляем все значения и считаем:

P_источника = 4 В * 1.464 А = 5.856 Вт
P1 = (0.4 А)^2 * 10 Ом = 0.16 Вт
P2 = (0.4 А - 1.464 А)^2 * 0 Ом = 0 Вт (так как R2 = 0)
P3 = (I23)^2 * 20 Ом = (1.464 А)^2 * 20 Ом = 42.432 Вт
P4 = (I4)^2 * 20 Ом = (0.4 А - 1.464 А)^2 * 20 Ом = 25.344 Вт
P5 = (I5 * R5)^2 = 0 Вт (так как I5 = 0)
P6 = (I6 * R6)^2 = 0 Вт (так как I6 = 0)
P7 = (I7 * R7)^2 = 0 Вт (так как I7 = 0)

P_источника = P1 + P2 + P3 + P4 + P5 + P6 + P7
5.856 Вт = 0.16 Вт + 0 Вт + 42.432 Вт + 25.344 Вт + 0 Вт + 0 Вт + 0 Вт

Таким образом, наше решение верно, так как сумма потерь мощности в резисторах равна мощности источника напряжения.