Дифракционная решетка с 150 штрихов в 1 мм помещен на расстоянии 50 см от экрана найдите расстояние до 3 фиолетового цвета

Дано:

N = 150

S = 1 мм = 1*10⁻³ м

L = 50 см = 0,5 м

m = 3

λ = 400 нм = 400*10⁻⁹ м

x - ?

1)

Находим постоянную решетки:

d = S / N = 1*10⁻³ / 150 ≈ 6,7*10⁻⁶ м

2)

Сделаем чертеж.

Для малых углов

sin α = tg α = x / L

Формула дифракционной решетки:

d*sin φ = m*λ

или

d*(tg φ) = m*λ

d*(x/L) = m*λ

x = m*λ*L/d = 3*400⁻⁹*0,5/ 6,7*10⁻⁶ ≈ 0,09 м   или   9 см

Возьмем длину волны фиолетового цвета равной 400нм.

Угол, под которым виден интерференционный максимум, можно найти из формулы:

,

где k - порядок максимума, λ- длина волны, d - период дифракционной решетки, который равен:

Для малых углов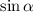 примерно равен tg α, который в свою очередь находится из прямоугольного треугольника, катетами которого являются расстояние до максимума x (противолежащий) и расстояние до экрана L (прилежащий).

Тогда: