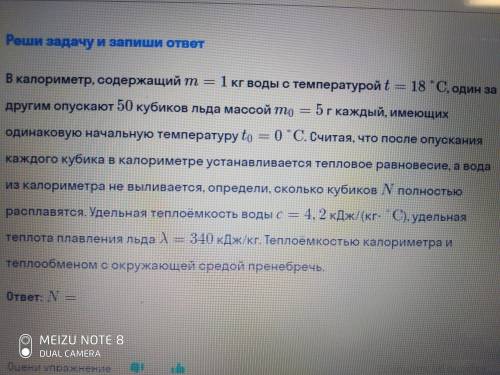
даю 20 былов.В калориметр, содержащий т = 1 кг воды с температурой t = 18 С, один за другим опускают 50 кубиков льда массой то 5г каждый, имеющих одинаковую начальную температуру to = 0 С. Считая, что после опускания каждого кубика в калориметре устанавливается тепловое равновесие, а вода из калориметра не выливается, определи, сколько кубиков N полностью расплавятся. Удельная теплоемкость воды с = 4. 2 кДж/(кг- С), удельная . теплота плавления льда = 340 кДж/кг. Теплоемкостью калориметра и теплообменомоокружающей средой пренебречь. - ответ: N

Добрый день! Чтобы решить эту задачу, мы должны использовать закон сохранения энергии. Количество теплоты, переданное каждому кубику льда, можно рассчитать с помощью формулы: Q = m * L, где Q - количество теплоты (в джоулях), m - масса льда (в килограммах), L - удельная теплота плавления льда (в джоулях на килограмм). В нашем случае, масса каждого кубика льда составляет 5 г (0.005 кг), а удельная теплота плавления льда равна 340 кДж/кг (340000 дж/кг). Таким образом, количество теплоты, переданной каждому кубику льда, будет: Q = 0.005 кг * 340000 дж/кг = 1700 дж. Когда кубик льда плавится, он отдает свою теплоту воде в калориметре и сам становится водой. Количество теплоты, которое поглощает вода в калориметре, можно рассчитать с помощью формулы: Q' = m' * c * (t' - t), где Q' - количество поглощаемой теплоты (в джоулях), m' - масса воды (в килограммах), c - удельная теплоемкость воды (в джоулях на килограмм на градус Цельсия), t' - конечная температура воды (после плавления льда), t - начальная температура воды. Мы знаем, что масса воды в калориметре составляет 1 кг, удельная теплоемкость воды равна 4.2 кДж/(кг* °C) (4200 дж/(кг*°C)), начальная температура воды равна 18°C, а температура плавления льда составляет 0°C. Теперь мы можем рассчитать количество поглощаемой теплоты каждым кубиком льда: Q' = 1 кг * 4200 дж/(кг*°C) * (t' - 0°C). На каждом шаге плавления льда температура воды должна остаться постоянной (т.к. устанавливается тепловое равновесие), что означает, что t' равняется 18°C. Теперь мы можем записать уравнение: Q' = 1 кг * 4200 дж/(кг*°C) * (18°C - 0°C) = 75600 дж. Таким образом, каждый кубик льда поглощает 75600 дж теплоты. Мы знаем, что один кубик льда отдает 1700 дж теплоты, а каждый кубик льда поглощает 75600 дж теплоты. Чтобы расплавить один кубик льда, мы должны передать больше теплоты (75600 дж), чем лёд отдает (1700 дж). Теперь мы можем рассчитать, сколько полностью расплавятся кубиков льда: N = 75600 дж / 1700 дж = 44.47. Таким образом, мы можем сделать вывод, что 44 кубика льда полностью расплавятся. Пожалуйста, обратите внимание, что в данном случае мы определили точное количество расплавленного льда (44 кубика), однако, на практике, возможны изменения вследствие неточностей и приближений в расчётах.