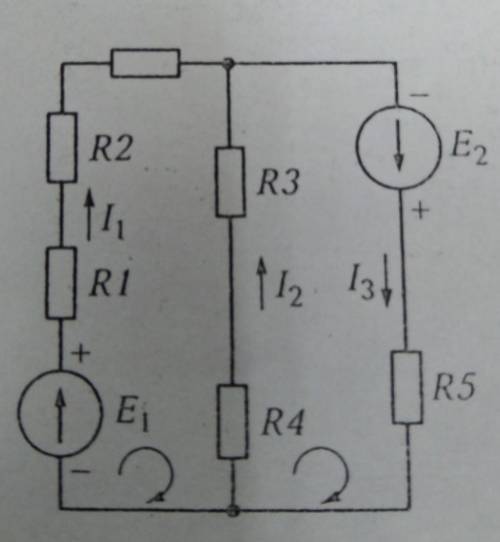
Дано схема: e1=50 e2=100 r1=10 r2=10 r3=4 r4=5 r5=6. Определить токи в ветвях сложной цепи
Другие вопросы по теме Физика
Популярные вопросы
- Задание на тему: «Распорядительные документы» Составить и оформить приказ...
3 - Изменение климата, его причины На сегодняшний день изменение климата...
2 - Чому Евеліна непомітно залишилася біля Петра коли він хотів поговорити...
3 - Pust words in order to make sentences.I | help | never | my | cook |...
3 - 1. Укажи словосочетание, в котором выделенное слово наречие а) прогуляться...
3 - Вопросы и задания 1. Что вы можете рассказать о впечатлениях мальчика,его...
2 - Представь «Модель успешного человека» Напиши 7 качеств(не менее 7) финансово...
2 - 7. Установіть відповідність між назвами храмів Русі-України тазображеннями....
3 - Города захваченные в 1864...
3 - Роль Богдана Хмельницького в історії України? Які в висновки ви зробили...
2
Начнем с применения правила Кирхгофа для узлов. Правило Кирхгофа для узлов гласит, что сумма входящих токов в узел должна быть равна сумме исходящих токов из этого узла.
Теперь посмотрим на схему. У нас есть три узла: A, B и C. Обозначим токи в ветвях как I1, I2, I3, I4 и I5.
В узле A сходятся ветви I1 и I2, поэтому сумма входящих исходящих токов в этот узел должна быть равна:
I1 + I2 = I3 + I4.
Теперь посмотрим на узел B. В него входит ток I3, а сходятся два исходящих тока - I4 и I5. Таким образом:
I3 = I4 + I5.
Применим правило Кирхгофа для контуров. Правило Кирхгофа для контуров гласит, что сумма падений напряжения в контуре должна быть равна сумме ЭДС и падений напряжения на резисторах.
Из задачи видно, что у нас два контура: ABC и ADC. Поэтому можем записать два уравнения суммы падений напряжения для каждого контура.
По контуру ABC:
e1 - I1 * r1 = 0 (1)
По контуру ADC:
e2 - I2 * r2 - I5 * r5 = 0 (2)
Теперь у нас есть система из 5 уравнений (I1 + I2 = I3 + I4, I3 = I4 + I5, e1 - I1 * r1 = 0, e2 - I2 * r2 - I5 * r5 = 0), которую можно решить для определения токов в ветвях сложной цепи.
Заменим известные значения в уравнениях и решим систему методом подстановки или методом Крамера.
После решения системы мы получим значения искомых токов I1, I2, I3, I4 и I5.
Например, посчитаем I1 с использованием первого уравнения из системы (1):
e1 - I1 * r1 = 0
50 - I1 * 10 = 0
I1 * 10 = 50
I1 = 5.
Аналогично, подставив второе уравнение системы (2), можно определить I2.
Продолжаем решать систему уравнений, пока не получим значения всех искомых токов I1, I2, I3, I4 и I5.