Дано: R1=5 ом
R2=12 ом
R3=6 ом
R4=10 ом
R5=15 ом
R6=3 ом
R7=4 ом
R8=2 ом
R9=6 ом
r=1 ом
p5=21,6 ом
найти:Rэкв;Е;I3;U1;p6
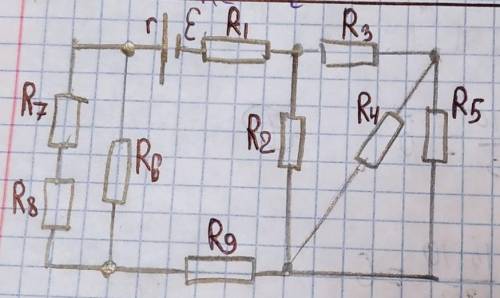
Другие вопросы по теме Физика
Популярные вопросы
- Папа купил три двух литровых покета молока м мама...
3 - Представьте в виде одночлена стандартного вида : -(-х^2у^4)^4*(6х^4*у)^2...
1 - Как с татарского на переводится слово хезмәт?...
2 - 20 ! в трапеции с основаниями 2 и 9 отрезок ке с концами на...
3 - Составить 5 предложений с частичкой не с существительными ....
2 - Выполните синтаксический разбор предложения- ветер свищет в...
2 - Диагонали трапеции перпендикулярны друг другу и равны соответсвенно...
3 - Выбрать some или any there is some/any milk in the fridge. are...
3 - Nh3+hi= и кристаллическая ришотка полученного вещества...
2 - 4. расскажите о том, как герасим муму. какое чувство вызвало...
1
Сначала давай найдем эквивалентное сопротивление Rэкв. Эквивалентное сопротивление - это общее сопротивление, которое было бы в цепи, если все сопротивления были заменены одним сопротивлением. Мы можем использовать формулу для сопротивлений, соединенных параллельно:
1/Rэкв = 1/R2 + 1/R4 + 1/R8
1/Rэкв = 1/12 + 1/10 + 1/2
1/Rэкв = (5/60 + 6/60 + 30/60) / 60
1/Rэкв = 41/60 / 60
1/Rэкв = 41/3600
Rэкв = 3600/41
Rэкв ≈ 87.8 ом
Теперь давай найдем напряжение Е в цепи. Мы можем использовать формулу для напряжения:
Е = I * Rэкв
Мы знаем, что I5 = p5 / R5
I5 = 21.6 / 15
I5 ≈ 1.44 A
Также мы знаем, что I1 = I5 + I6
I1 = I5 + U1 / R1
I1 = 1.44 + U1 / 5
I1 ≈ 1.44 + U1 / 5
I1 ≈ 1.44 + U1 / 5
Теперь мы можем использовать закон Ома для найти напряжение U1:
U1 = I1 * R1
U1 = (1.44 + U1 / 5) * 5
U1 = 7.2 + U1
U1 - U1 = 7.2
U1 = 7.2 В
Теперь мы можем найти I1:
I1 = I5 + U1 / R1
I1 ≈ 1.44 + 7.2 / 5
I1 ≈ 1.44 + 1.44
I1 ≈ 2.88 А
Мы можем использовать закон Ома еще раз для найти напряжение U3:
U3 = I3 * R3
Мы не знаем I3, но мы можем использовать закон Кирхгофа для напряжений в замкнутом контуре:
U1 = U2 + U5
U1 = I1 * R1
U2 = I2 * R2
U5 = I5 * R5
Учитывая, что U1 = 7.2 В и U5 = 21.6 В (из данных), мы можем найти U2:
U2 = U1 - U5
U2 = 7.2 - 21.6
U2 = -14.4 В
Теперь мы можем использовать закон Ома, чтобы найти I2:
I2 = U2 / R2
I2 = -14.4 / 12
I2 = -1.2 А
Обратите внимание, что получили отрицательную величину для тока I2. Это означает, что направление тока I2 в схеме не так, как мы предполагали. Поэтому, чтобы рассчитать I3, мы должны использовать тот факт, что сумма токов, входящих в узел, равна сумме токов, покидающих узел:
I1 = I2 + I3
2.88 = -1.2 + I3
I3 = 2.88 + 1.2
I3 ≈ 4.08 А
Наконец, давай найдем p6:
p6 = I6^2 * r
I6 = I1 - I5
I6 ≈ 2.88 - 1.44
I6 ≈ 1.44 А
p6 = 1.44^2 * 1
p6 ≈ 2.07 Вт
Итак, ответы на задачу:
Rэкв ≈ 87.8 ом
Е ≈ 7.2 В
I3 ≈ 4.08 А
U1 ≈ 7.2 В
p6 ≈ 2.07 Вт
Надеюсь, это наглядное и подробное объяснение помогло тебе понять решение задачи. Если у тебя возникнут еще вопросы, не стесняйся задавать!"