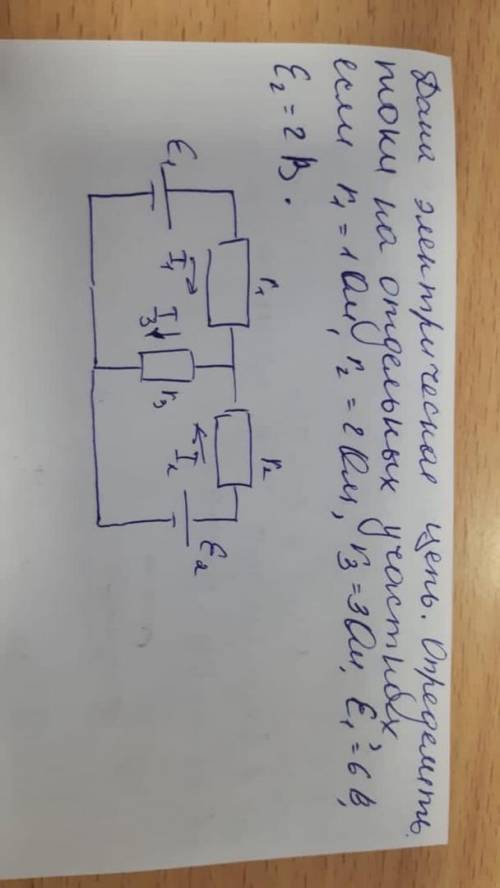
Дана электрическая цепь определить токи на отдельных участках если r1=1 ом r2=2ом r3=3ом e1=6в e2=2в

Для решения этой задачи по определению токов на отдельных участках в электрической цепи, мы можем использовать законы Кирхгофа.

Законы Кирхгофа включают закон Кирхгофа о сумме токов в узле (первый закон Кирхгофа) и закон Кирхгофа о сумме падений напряжения в замкнутом контуре (второй закон Кирхгофа).

Давайте выразим данные величины и токи на отдельных участках задачи.

У нас есть следующие данные:
r1 = 1 ом - сопротивление первого участка
r2 = 2 ома - сопротивление второго участка
r3 = 3 ома - сопротивление третьего участка
e1 = 6 В - напряжение в источнике e1
e2 = 2 В - напряжение в источнике e2

Теперь построим электрическую цепь и обозначим неизвестные токи на отдельных участках: I1, I2 и I3.



По первому закону Кирхгофа, сумма токов, входящих в узел, равна сумме токов, выходящих из узла. В данной задаче у нас есть только один узел, поэтому можем записать:

I1 + I2 = I3

По второму закону Кирхгофа, сумма падений напряжения в замкнутом контуре равна сумме ЭДС в этом контуре. Рассмотрим петлю ABCD:

По пути A-B-E1-C-A сумма падений напряжения равна ЭДС в источнике e1, поэтому:

I1 * r1 + I2 * r2 = e1

По пути B-C-E2-D-B сумма падений напряжения равна ЭДС в источнике e2, поэтому:

I2 * r2 + I3 * r3 = e2

У нас теперь есть система уравнений, состоящая из двух уравнений:

I1 + I2 = I3 (1)
I1 * r1 + I2 * r2 = e1 (2)
I2 * r2 + I3 * r3 = e2 (3)

Выразим I1 из уравнения (1):

I1 = I3 - I2

Подставим найденное значение I1 в уравнение (2):

(I3 - I2) * r1 + I2 * r2 = e1

Раскроем скобки и упростим:

I3 * r1 - I2 * r1 + I2 * r2 = e1

Перенесем все члены с I2 влево и сгруппируем:

I3 * r1 + I2 * (r2 - r2) = e1

I3 * r1 = e1

Выразим I3 из этого уравнения:

I3 = e1 / r1

Подставим найденное значение I3 в уравнение (3):

I2 * r2 + (e1 / r1) * r3 = e2

Упростим:

I2 * r2 + e1 * (r3 / r1) = e2

Выразим I2 из этого уравнения:

I2 = (e2 - e1 * (r3 / r1)) / r2

Теперь, зная значения I2 и I3, мы можем найти I1, подставив эти значения в уравнение (1):

I1 = I3 - I2

Итак, мы нашли значения токов на отдельных участках в электрической цепи задачи. Чтобы посчитать конкретные численные значения, необходимо подставить известные значения сопротивлений и напряжений в полученные уравнения.