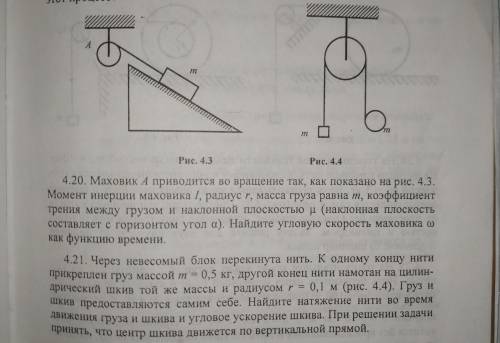
Через невесомый блок перекинута нить. К одному концу нити прикреплен груз массой т = 0,5 кг, другой конец нити намотан на цилиндрический шкив той же массы и радиусом r = 0,1 м (рис. 4.4). Груз и Шкив предоставляются самим себе. Найдите натяжение нити во время движения груза и шкива и угловое ускорение шкива. При решении задачи принять, что центр шкива движется по вертикальной прямой не могу понять, как будут связаны ускорения
Другие вопросы по теме Физика
Популярные вопросы
- Найдите значение выражений: а) 3/5-1/4+1/3= б)(2/3+1/9)-13/18 в)5/6-2/3+1/4...
3 - 1. орган дыхания улитки a) жабры b) мантия c) трахея d)кожа e) лёгкие...
3 - Водолаз в жестком скафандре может погружаться на глубину 250 м, а опытный...
2 - Какая пара прилагательных не является антонимами? а) пологий – крутой...
2 - Пройдя половину маршрута турист увиличел скорость 25% и поэтому пробыл...
2 - Взоопарке было 12 куропатак,15 глухорей,а тетеровов столько,сколько...
3 - Характеристика одного из героев комедии ревизор...
2 - Выпишите из текста слова с безударный гласной в корне: текст: как прохладно...
2 - Напишити обложжку к произведению постойко...
1 - Солнце нагревает только верхний слой океана толщиной в несколько метров....
2
1. Найдем натяжение нити:
Натяжение нити будет равно силе тяжести, действующей на груз, так как груз находится в состоянии равновесия вертикального движения:
F = m*g, где m - масса груза, g - ускорение свободного падения (примем g = 9,8 м/с²).
F = 0,5 кг * 9,8 м/с² = 4,9 Н.
2. Найдем угловое ускорение шкива:
2.1 Найдем силу, действующую на шкив.
Сила, действующая на шкив, равна силе натяжения нити, так как нить невесомая и сила натяжения одинакова в любой точке нити:
F = 4,9 Н.
2.2 Найдем момент силы, действующий на шкив.
Момент силы, действующий на шкив, равен произведению силы на радиус шкива:
M = F * r, где r - радиус шкива.
M = 4,9 Н * 0,1 м = 0,49 Н*м.
2.3 Найдем угловой момент инерции шкива.
Угловой момент инерции шкива можно рассчитать по формуле для цилиндра:
I = 0,5 * m * r², где m - масса шкива, r - радиус шкива.
m = 0,1 кг (условие задачи).
I = 0,5 * 0,1 кг * (0,1 м)² = 0,0005 кг*м².
2.4 Найдем угловое ускорение шкива.
Угловой момент инерции связан с угловым ускорением шкива следующим образом:
τ = I * α, где τ - момент силы, I - угловой момент инерции, α - угловое ускорение.
0,49 Н*м = 0,0005 кг*м² * α.
α = 0,49 Н*м / 0,0005 кг*м² = 980 рад/с².
Таким образом, натяжение нити равно 4,9 Н, а угловое ускорение шкива равно 980 рад/с².