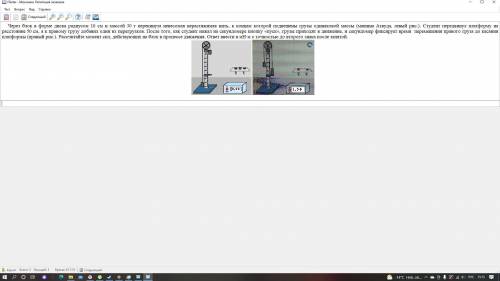
Через блок в форме диска радиусом 10 см и массой 30 г перекинута невесомая нерастяжимая нить, к концам которой подвешены грузы одинаковой массы (машина атвуда, левый рис.). студент передвинул платформу на расстояние 50 см, а к правому грузу добавил один нз перегрузков. после того, как студент нажал на секундомере кнопку «пуск», грузы приходят в движение, н секундомер фикснрует время перемещения правого груза до касания платформы (правый рис.). рассчитайте момент сил, действуюших на блок в процессе движения. ответ ввести в мнгм с точностью до второго знака после запятой.

Для решения данной задачи нам нужно рассчитать момент сил, действующих на блок в процессе движения.

Для начала, давайте разберемся, какие силы действуют на блок. Основными силами, действующими на блок, являются сила натяжения нити и сила трения.

Сила натяжения нити может быть определена как сила тяжести двух грузов, подвешенных на ней, так как эти силы полностью компенсируют друг друга. Масса каждого груза равна массе машины Атвуда, то есть 30 г.

Таким образом, суммарная масса грузов, воздействующая на блок, равна 2 * 30 г = 60 г = 0,06 кг.

Сила трения будет действовать на блок, так как он соприкасается с платформой и будет иметь тенденцию остановиться. Она направлена противоположно направлению движения блока.

Теперь мы можем рассчитать момент силы, используя известные нам значения радиуса блока и сил, действующих на него.

Момент силы (M) может быть рассчитан по формуле: M = r * F * sin(θ), где r - радиус блока, F - сила, действующая на блок, θ - угол между вектором силы и вектором радиуса блока.

Так как сила трения направлена в противоположную сторону движения блока, угол между вектором силы трения и вектором радиуса блока составляет 180 градусов (полный угол).

Таким образом, момент силы, действующий на блок, будет равен: M = r * F * sin(180°).

Угол 180 градусов эквивалентен радианной мере π радиан.

Обратите внимание, что sin(π) = 0.

Поэтому, момент силы, действующей на блок, будет равен 0.

Итак, ответ на ваш вопрос: момент силы, действующих на блок в процессе движения, равен 0 мН*м.