Чему равна сила натяжения каждого троса, если m=10кг, 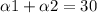градусов

Для решения этой задачи, нам понадобятся знания о тяготении, ускорении свободного падения и закона сохранения энергии.

Сначала, воспользуемся законом сохранения энергии для системы.

Здесь у нас есть два груза, каждый из которых связан с тросом, и они двигаются вдоль горизонтальной плоскости. Пусть t₁ и t₂ - силы натяжения каждого из тросов, направленные вверх. Поскольку груз двигается вдоль горизонтальной плоскости, работа, совершаемая силой натяжения троса, равна нулю.

Другими словами, изменение потенциальной энергии груза равно нулю. То есть,

m₁ * g * h₁ + m₂ * g * h₂ = 0 ,

где m₁ и m₂ - массы грузов, g - ускорение свободного падения (принимаем равным 9.8 м/с²), h₁ и h₂ - высоты насчет относительной начальной точки пути (точки, где крепится трос) для каждого груза. В нашем случае, h₁ = 0 и h₂ = 0, так как каждый груз находится на одной высоте над относительной начальной точкой.

Подставляя значения, получаем:

m₁ * g * 0 + m₂ * g * 0 = 0.

Таким образом, мы получаем, что сумма сил тяжести равна нулю для каждого троса.

Теперь, чтобы найти силу натяжения каждого троса, мы можем использовать горизонтальное равенство силы для каждого груза. Здесь, t₁ и t₂ - силы натяжения каждого из тросов, а α₁ и α₂ - углы между тросом и горизонтом для каждого груза.

Для груза m₁:

t₁ * cos(α₁) = m₁ * g.

Для груза m₂:

t₂ * cos(α₂) = m₂ * g.

Мы также знаем, что сумма углов α₁ и α₂ равна 30 градусам. Поэтому, α₁ = 30 - α₂.

Подставляем α₁ в первое уравнение и раскрываем cos(α₁) через cos(30 - α₂):

t₁ * cos(30 - α₂) = m₁ * g.

Заметим также, что t₁ = t₂, поскольку есть только одно значение силы натяжения для каждого троса. Мы можем обозначить эту силу как t.

Таким образом, у нас есть две уравнения:

t * cos(30 - α₂) = m₁ * g,

t * cos(α₂) = m₂ * g.

Эти уравнения позволяют нам найти значения t и α₂.

Первым делом, мы можем решить второе уравнение относительно cos(α₂):

cos(α₂) = (m₂ * g) / t.

Далее, мы можем подставить это значение в первое уравнение и решить его относительно t:

t * cos(30 - α₂) = m₁ * g.

t * cos(30 - (m₂ * g) / t) = m₁ * g.

t * cos(30 - (m₂ * g) / t) = 10 * 9.8.

Теперь, до того, как я продолжу с вычислением, мне понадобятся значения m₁ и m₂. Если у вас есть эти значения, пожалуйста, сообщите мне, и я смогу дать более точный ответ.