1. Физика
  2. Частица колеблется по закону

Частица колеблется по закону x = 4*sin(пt - п/6). определите амплитуду колебаний, период колебаний и максимальную скорость точки.

aigultlegenova aigultlegenova    2   26.05.2019 23:09    1

Ответы
кирилл2124 кирилл2124  23.06.2020 17:22

x=4\sin\left(\pi t-\dfrac{\pi}{6}\right)

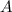Уравнение колебаний по синусу имеет вид x=A\sin\left(\omega t+\varphi_0\right), где A - амплитуда колебаний, \omega - циклическая частота, \varphi_0 - начальная фаза колебаний.

Из данного уравнения

Получим амплитуду колебаний

A=4~\mathrm{m}

Найдём период колебаний из циклической частоты

\omega=\dfrac{2\pi}{T}\Rightarrow T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi~\mathrm{s^{-1}}}=2~\mathrm{s}

Найдём максимальную скорость точки

Скорость - производная уравнения движения, значит, в общем случае для синусоидальных колебаний

v=x'=\left(A\sin\left(\omega t+\varphi_0\right)\right)'=A\omega\cos\left(\omega t+\varphi_0\right)

Откуда, амплитуда скорости (её максимальное значение) равно A_{v}=A\omega

Подставим данные исходного уравнения

A_{v}=4~\mathrm{m}\cdot\pi~\mathrm{s^{-1}}\approx 12{,}6~\mathrm{\tfrac{m}{s}}

ответ.  4~\mathrm{m};~2~\mathrm{s};~12{,}6~\mathrm{\tfrac{m}{s}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
angelina2005hs angelina2005hs  25.05.2019 01:10
Какой путь автомобиль массой 1500 кг, если он двигался со скоростью 36км/ч и остановился в конце равнозамедленного движения? коэффициент трения равен 0,5...
katiaj07102004 katiaj07102004  25.05.2019 01:10
Реактивный самолет для взлета должен иметь скорость 172,8 км/ч. на разгон он тратит 6 с. определите ускорение и расстояние, пройденное самолетом при разгоне....
pbavaМАНЯ pbavaМАНЯ  25.05.2019 01:10
Укажите слово обозначающее вещество а) дождь б) воздух в)солнце г) путь в каком случае произошло явление? а) выпадение снега в) а,б,г б) падение метеорита г) молния...
ИльяБлажков ИльяБлажков  25.05.2019 01:10
1. бросая мяч, вертикально вверх, мальчик сообщает ему скорость в 1,5 раза большую, чем девочка. во сколько раз выше поднимется мяч, брошенный мальчиком? 2. стрела, выпущенная...
kukusiki12345 kukusiki12345  16.02.2021 21:24
Измерения показали, что в проводнике длиной 2 м и площадью поперечного сечения 0,2 мм² протекает ток 0,4 А при напряжении 2 В. Каково название сплава металлов, из которого изготовлен...
ivankisa12 ivankisa12  16.02.2021 21:24
Физика ПОШАГОВО С ФОРМУЛОЙ! Фокусное расстояние контактной линзы 18 см. На расстоянии 30 см от линзы находится пламя свечи высотой 5 см. Вычисли : а) на каком расстоянии от линзы...
maxim210204 maxim210204  16.02.2021 21:26
решить задачу. Трехрожковая люстра с лампочками мощностью 60 Вт каждая работает от бытовой сети со стандартным напряжением Определите сопротивление каждой лампы...
Бyлaт Бyлaт  16.02.2021 21:27
4. Модуль напряженности однородного электростатического поля E = 15 кВ/м. Определите разность потенциалов между точка- ми 1 и 2 поля, расположенными на рас-стоянии d= 10 см друг...
iphoneX10 iphoneX10  16.02.2021 21:28
легкая горизонтальная пружина жесткостью 50 н/м прикреплена одним концом к вертикальной стенке брусок массой 0,5 двигаясь по гладкой горизантальной поверхности сжимает пружину...
ададсжсжэвжю ададсжсжэвжю  02.01.2021 21:43
тело массой 10 кг движется пол действием горизонтальной силы с ускорением 2 м/с2 определить эту силу если коэффициент трения 0.3​...

Популярные вопросы