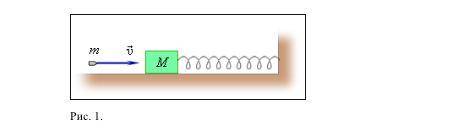
Брусок массой M = 0,5 кг, лежащий на гладкой горизонтальной поверхности, прикрепили пружиной к стене (см. рис.). В брусок попадает пуля из духового ружья массой m = 5 г, летящая горизонтально со скоростью υ = 100 м/с. Брусок вместе с застрявшей в нём пулей начинает колебаться с амплитудой xmax = 10 см. Определите период T этих колебаний.

Для определения периода колебаний бруска с пулей внутри, мы можем использовать закон сохранения энергии.

В начальный момент времени, когда пуля попадает в брусок, вся кинетическая энергия пули превращается в потенциальную энергию пружины. Когда брусок достигает максимального отклонения xmax, всё состояние кинетической энергии превращается в потенциальную энергию пружины, и наоборот.

Масса пули: m = 5 г = 0,005 кг
Скорость пули: υ = 100 м/с
Масса бруска: M = 0,5 кг
Максимальное отклонение бруска: xmax = 10 см = 0,1 м

Для начала, мы можем найти скорость пули в момент попадания в брусок.

Поскольку нет горизонтальных сил (пуля движется по горизонтальной поверхности), горизонтальная составляющая импульса пули должна сохраняться. Импульс пули равен произведению массы на скорость:

Im = m * υ = 0,005 кг * 100 м/с = 0,5 кг * м/с

Когда пуля попадает в брусок, она останавливается, и ее импульс полностью передается бруску. Следовательно, импульс бруска будет равен импульсу пули:

Im = M * V

где V - скорость бруска. Мы также знаем, что начальная кинетическая энергия пули становится потенциальной энергией пружины, поэтому мы можем записать:

(1/2) * m * υ^2 = (1/2) * k * xmax^2

где k - коэффициент жесткости пружины.

Используя скорость бруска, равную импульсу пули, разделенной на массу бруска, мы можем найти значение коэффициента жесткости пружины:

k = (M * V^2) / xmax^2

Теперь, чтобы найти период колебаний, мы можем использовать уравнение периодических колебаний:

T = 2π * √(m_eff / k)

где m_eff - эффективная масса системы, которая включает массу бруска и пули, и вычисляется как:

m_eff = M + m

Теперь у нас есть все необходимые значения, чтобы найти период колебаний.

Подставим числовые значения:

m_eff = 0,5 кг + 0,005 кг = 0,505 кг

k = (0,5 кг * (0,5 кг * м/с)^2) / (0,1 м)^2 = 12,5 Н/м

Теперь можем вычислить период:

T = 2π * √(0,505 кг / 12,5 Н/м) ≈ 0,898 с

Таким образом, период колебаний составляет примерно 0,898 секунды.