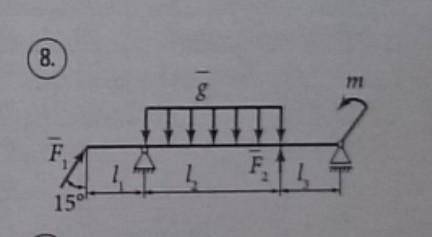
Балки на двух опорах нагружены сосредоточенными силами F1 и F2, распределенной нагрузкой g и парой сил с моментом m. Определить реакции опор. С решением. F1 = 9 kH, F2 = 4 kH, g = 65 kH/м, m = 26 kH * м, l1 = 4 м, l2 = 1 м, l3 = 4 м.​

Для решения данной задачи сначала определим полные нагрузки на каждую балку. Затем, используя условие равновесия моментов и сил, найдем реакции опор.

Первая балка:

1. Рассмотрим силы, действующие на первую балку:
- Сосредоточенная сила F1 (9 kH), действующая на расстоянии l1 (4 м) от первой опоры.
- Распределенная нагрузка g (65 kH/м), действующая на всей длине балки.
- Пара сил с моментом m (26 kH * м), действующая на расстоянии l2 (1 м) от первой опоры.

2. Найдем полную нагрузку на первую балку:
- Посчитаем момент относительно оси первой опоры: M = F1 * l1 + m * l2.
- Действующая на всей длине балки распределенная нагрузка превращается в сосредоточенную силу, равную площади под кривой распределенной нагрузки умноженной на длину балки. В данном случае, площадь под кривой равна (g * l1) / 2, так как треугольник.

Таким образом, полная нагрузка на первую балку равна:
- Полная сосредоточенная сила: F1.
- Полная распределенная нагрузка: (g * l1) / 2.
- Момент: M.

Вторая балка:

1. Рассмотрим силы, действующие на вторую балку:
- Сосредоточенная сила F2 (4 kH), действующая на расстоянии l3 (4 м) от второй опоры.
- Распределенная нагрузка g (65 kH/м), действующая на всей длине балки.

2. Найдем полную нагрузку на вторую балку:
- Распределенная нагрузка умноженная на длину балки.

Таким образом, полная нагрузка на вторую балку равна:
- Полная сосредоточенная сила: F2.
- Полная распределенная нагрузка: g * l3.

Определение реакций опор:

1. Для определения реакций опор рассмотрим равновесие моментов и сил по двум осям: вертикальной и горизонтальной.

2. По горизонтальной оси (ось x) реакция первой опоры (A):
- Сумма всех моментов равна нулю.
- В данном случае, есть только один момент, вызванный сосредоточенной силой F2, действующей на расстоянии l3 от второй опоры:
M(A) = F2 * l3.
- Реакция первой опоры: A = -M(A) / l1.

3. По вертикальной оси (ось y) сумма вертикальных сил равна нулю:
- Реакция второй опоры (B) найдется как разница между вертикальной компонентой силы F1 и вертикальной компонентой полной нагрузки на первую балку.

Таким образом, мы можем определить реакции опор:
- Реакция первой опоры (A): A = -F2 * l3 / l1.
- Реакция второй опоры (B): B = F1 - (g * l1) / 2 - F2.

Надеюсь, это решение поможет вам понять, как найти реакции опор в данной задаче. Если у вас остались вопросы, не стесняйтесь задавать их.