1. Физика
  2. Автомобиль движется по горизонтальной

Автомобиль движется по горизонтальной дороге со скоростью 12,5 м/с. после выключения двигателей он остановился через 625 м. определите коэффициент трения

Vica73751 Vica73751    3   27.09.2019 04:30    4

Ответы
leha201711goruinov leha201711goruinov  08.10.2020 21:55

Дано:

v_{0} = 12,5 м/с

v = 0 м/с

s = 625 м

g = 10 м/с²

======================

Найти: \mu - ?

======================

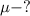
Решение. Определим, с каким ускорением останавливался автомобиль:

a = \frac{v^{2} - v_{0}^{2}}{2s}.

По второму закону Ньютона: F = m|a| = m|\frac{(v^{2} - v_{0}^{2})}{2s}|.

Сила трения определяется по формуле: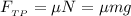 F_{_{TP}} = \mu N = \mu mg.

По третьему закону Ньютона: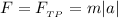 F = F_{_{TP}} = m|a|.

Приравняем значения этих сил и выразим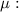 \mu:

m|\frac{(v^{2} - v_{0}^{2})}{2s}| = \mu mg \Rightarrow \boxed {\mu = \frac{1}{g}|\frac{(v^{2} - v_{0}^{2})}{2s}|}.

Определим значение искомой величины:

\mu = \frac{1}{10} \cdotp |\frac{0^{2} - 12,5^{2}}{2 \cdotp 625}| = \frac{1}{10} \cdotp \frac{1}{8} = \frac{1}{80} = 0,0125.

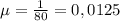ответ: \mu = \frac{1}{80} = 0,0125.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
гамов666 гамов666  23.05.2020 11:11
Какую мощность развивает мотор игрушечной машинки , если за 12 мин он совершает работу 1800 дж ? Кто даст ответ , вы можете не пытаться списать это с другого ответа с других сайтов...
sofia200000 sofia200000  22.05.2020 20:25
Шкільний вольтметр має опір 2,3 Ом і може вимірювати напругу 15 В. Якої довжини ніхромову дротину, переріз якої дорівнює 1 мм2, слід до нього приєднати, щоб збільшити межі вимірювання...
DariaMolotova DariaMolotova  23.05.2020 11:23
K50-16±5% КАКОВ КЛАСС ТОЧНОСТИ ЭТОГО КОНДЕНСАТОРА? 1) 50% 2) 16% 3) 2% 4) 5%...
funnybotan2000 funnybotan2000  23.05.2020 11:24
Газ, що займав об’єм 560 л за температури 280 К, нагріли до 295 К. Визначте роботу, виконану газом, якщо процес відбувався за сталого тиску 1 МПа....
animator351 animator351  22.05.2020 10:30
Как изменится емкость при увеличении длины кабеля? сопротивление увеличивается. вместе с ней и реактивная? С=q/U уменшается?...
Marinka29082004 Marinka29082004  22.05.2020 20:48
Значение знака (g) в формуле по физике F= mg*h/l+Fтр....
Iruna131 Iruna131  22.05.2020 10:30
Установіть відповідність між : а) Важіль 1. блок, що піднімається й опускається разом з вантажем б) Блок 2. тверде тіло, яке може обертатися навколо нерухомої осі в) Рухомий блок 3....
kruglov428 kruglov428  02.02.2021 17:15
Масса машины с грузом 7000кг. Для того,чтобы она начала равномерное движение, действует сила 35 кН. Определите коэффициент трения между колесом машины и поверхностью дороги (0,5)​...
SvetaMew SvetaMew  02.02.2021 17:15
производите при ходьбе и какое -- стоя на месте. полных квадратиков, попавших внутрь контура, и прибавьте к немуполовину числа неполных квадратиков, через которые ли.ния контура. Полученное...
alenakoslova alenakoslova  02.02.2021 17:15
решить задачу по физике: какова плотность азота при давлении 100 кПа и температуре 45°С ?​...

Популярные вопросы