№ 9. В вершинах квадрата со стороной 10 см расположены три отрицательных и один положительный заряд 70 нКл каждый. Квадрат находится в воздухе. Определите напряженность поля в центре квадрата. ответ: В/м.​

Е=252 кВ/м

Объяснение:

Поскольку два противоположные заряды положительный и отрицательный. В сумме получается 0.

Поэтому в центре q=q₁+q₂=2q₁

А напряженность

Е=к*2*2q₁/а²=9*10⁹*4*70*10⁻⁹/0,1²=4*63000=252 кВ/м

Расстояние от центра квадрат до заряда = половине диагонали =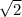 а/2

квадрат расстояния =2а²/4=а²/2

Если подставить это число в формулу 2 будет в числителе

Добрый день!
Чтобы определить напряженность поля в центре квадрата, нам понадобится сначала посчитать величину электрического поля в точке, а затем разделить эту величину на расстояние до этой точки.
Для начала, вспомним формулу для вычисления величины электрического поля от точечного заряда:

E = k * Q / r^2

где E - величина электрического поля, k - постоянная Кулона, Q - величина заряда, а r - расстояние от заряда до точки.

В данной задаче у нас есть три отрицательных заряда и один положительный заряд, поэтому мы должны сперва вычислить величину поля от каждого заряда и затем сложить их.

Приступим к расчетам.
Первый отрицательный заряд:
E1 = k * (-70 нКл) / (10 см)^2
= 9 * 10^9 * (-70 * 10^-9) / (0.1 м)^2

Затем мы переходим к следующему отрицательному заряду:
E2 = k * (-70 нКл) / (10 см)^2
= 9 * 10^9 * (-70 * 10^-9) / (0.1 м)^2

И, наконец, вычисляем поле от положительного заряда:
E3 = k * (70 нКл) / (10 см)^2
= 9 * 10^9 * (70 * 10^-9) / (0.1 м)^2

Затем, чтобы получить полную величину поля в центре, мы складываем эти значения:

E_общ = E1 + E2 + E3

И, наконец, чтобы определить напряженность поля в центре квадрата, мы делим E_общ на расстояние от центра квадрата до точки:

E_центр = E_общ / (0.1 м)

Подставляем значения и вычисляем:

E1 = 9 * 10^9 * (-70 * 10^-9) / (0.1 м)^2
E2 = 9 * 10^9 * (-70 * 10^-9) / (0.1 м)^2
E3 = 9 * 10^9 * (70 * 10^-9) / (0.1 м)^2

E_общ = E1 + E2 + E3

E_центр = E_общ / (0.1 м)

Только после выполнения всех этих расчетов мы сможем получить искомый ответ: значение напряженности поля в центре квадрата.