1. Физика
  2. 3. тело свободно падает с

3. тело свободно падает с высоты 125м. какой путь тело
пройдёт за последнюю секунду движения. за сколько времени тело
пройдёт первые 80м? ​

амаеру амаеру    2   11.07.2019 14:26    15

Ответы
azilhan1 azilhan1  17.09.2020 21:47

Сначала определим время падения, g=10м/с^2

Формула S=gt^2/2

Отсюда t^2=2S/g

t = \sqrt{ \dfrac{2s}{g} } \\ t = \sqrt{ \frac{250}{10} } = \sqrt{25} = 5

[t]=кв. корень из м*с^2/м=с

Первые 80 метров тело пройдет за 4 секунды (пользуясь этой же формулой),

t = \sqrt{ \dfrac{160}{10} } = \sqrt{16} = 4

А за последнюю, 5-ю секунду тело пройдет 125-80=45 м.

ПОКАЗАТЬ ОТВЕТЫ
Inozemceva1981 Inozemceva1981  17.09.2020 21:47
Дано:

Высота падения: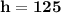 \bf h = 125 м.

Начальная скорость отсутствует: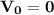 \bf V_0 = 0 м/с.

Ускорение свободного падения: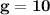 \bf g = 10 м/с².

Найти нужно:

1) Путь за последнюю секунду: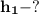 \bf h_1 - ?

2) Время прохождения первых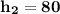 \bf h_2 = 80 м высоты: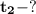 \bf t_2 - ?

Решение:

1. Найдём время падения: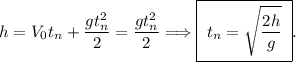 h = V_0t_n + \dfrac{gt_n^2}{2} = \dfrac{gt_n^2}{2} \Longrightarrow \boxed{\;t_n = \sqrt{\dfrac{2h}{g}}\;}.

2. Найдём путь за последнюю секунду, как разность общей высоты падения и пройденной высоты за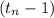 (t_n - 1) секунду: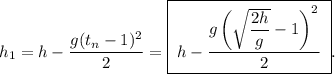 h_1 = h - \dfrac{g(t_n-1)^2}{2} = \boxed{\;h - \dfrac{g\left(\sqrt{\dfrac{2h}{g}}-1\right)^2}{2}\;}.

3. Время прохождения высоты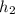 h_2 ищется аналогично первому действию: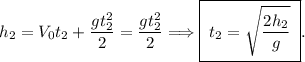 h_2 = V_0t_2 + \dfrac{gt_2^2}{2} = \dfrac{gt_2^2}{2} \Longrightarrow \boxed{\;t_2 = \sqrt{\dfrac{2h_2}{g}}\;}.

Численно получим: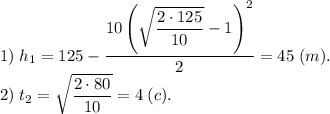

1)\; h_1 = 125 - \dfrac{10\left(\sqrt{\dfrac{2\cdot125}{10}}-1\right)^2}{2} = 45 \;(m).\\2)\; t_2 = \sqrt{\dfrac{2\cdot80}{10}} = 4\; (c).

ответ: 45 м, 4 с.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
licicha licicha  01.03.2021 14:11
У вершинах A і B прямокутного трикутника ABC (кут C — прямий) перебувають заряди qA=20нКл і qB=60нКл. Довжини катетів AC і BC дорівнюють відповідно а і 10 см. Напруженість електричного...
dashechka1707 dashechka1707  01.03.2021 14:11
О БОЖЕ ВАС Выберите положение тела, в котором оно производит наибольшее и наименьшее давление. Напишите ответ, используя слова давление, площадь, сила.​...
Esenbekmalika30 Esenbekmalika30  22.08.2019 07:30
Определите число молекул в 1 см^3 воды....
СГлазамиЦветаСчастья СГлазамиЦветаСчастья  22.08.2019 07:30
Сила тока в утюге 0,2 а. какой электрический заряд пройдёт через спираль за 5 минут...
Ragman007 Ragman007  22.08.2019 07:30
Как изменяется давление газа при его нагревании и сжатии...
lt20 lt20  22.08.2019 07:30
Тело массой m=0.5кг движется вlоль оси ox под действием двух сил f1 и f2, направленных вдоль оси. зависимости проекции скорости тела на ось ox от времени имеет вид ux = a+bt,...
ler22kya ler22kya  22.08.2019 07:30
Чи притягує землю літак, що летить?...
кристина1423 кристина1423  22.08.2019 07:30
Яка сила утримує тіла на поверхні землі?...
vvbedash vvbedash  22.08.2019 07:30
Опять решить мне . нужно сегодня.буду - . 1. f1=70kh f2=1500h l3=2м найти l1-? 2. f1=65h l1=20см l2=500мл найти f2-? 3. f2=100h l1=0,3 l2=85см найти f1-?...
sleta1998A sleta1998A  22.08.2019 07:30
За жорсткістю 96 н/м брусок масою 2,4 кг рівномірно тягнуть по столу. яким є видовження пружини, якщо коефіцієнт тертя між бруском і столом дорівнює 0,...

Популярные вопросы