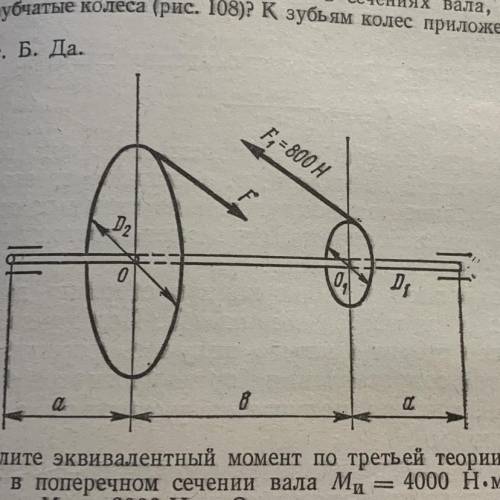
3. Определить диаметр вала (по третьей теории прочности) по рис. 108. Силы F1 и F2, расположены в параллельных плоскостях: D1= 200 мм; D2, =
= 400 мм; а = 300 мм; b= 400 мм; материал вала — сталь 40; [о] = 60 Н/мм2
(МПа).

Для определения диаметра вала по третьей теории прочности, мы должны рассчитать суммарный момент сил, действующих на вал, и проверить, что это значение не превышает предельное значение изгибающего напряжения материала вала.

Шаг 1: Определение суммарного момента сил
Для начала, нам нужно определить момент каждой силы, F1 и F2. Момент силы определяется путем умножения силы на расстояние до оси вращения.

Момент силы F1 = F1 * a
Момент силы F2 = F2 * (b-a)

Шаг 2: Вычисление суммарного момента сил
Суммарный момент сил будет равен сумме моментов каждой силы:
Мсумм = МF1 + МF2

Шаг 3: Определение предельного изгибающего напряжения материала
Предельное изгибающее напряжение материала вала необходимо получить из предоставленных данных.
[о] = 60 Н/мм2 = 60 МПа

Шаг 4: Определение диаметра вала
А теперь мы можем использовать формулу третьей теории прочности для определения диаметра вала:
Мсумм ≤ ((π * d^3) / 16) * [о]

Давайте выполним все эти шаги по порядку:

Шаг 1: Определение момента каждой силы
Момент F1 = F1 * a
Момент F1 = 2000 Н * 300 мм = 600 000 Н * мм = 600 Н * м

Момент F2 = F2 * (b-a)
Момент F2 = 4000 Н * (400 мм - 300 мм) = 4000 Н * 100 мм = 400 000 Н * мм = 400 Н * м

Шаг 2: Вычисление суммарного момента сил
Мсумм = МF1 + МF2
Мсумм = 600 Н * м + 400 Н * м
Мсумм = 1000 Н * м

Шаг 3: Определение предельного изгибающего напряжения материала
[о] = 60 МПа

Шаг 4: Определение диаметра вала
Мсумм ≤ ((π * d^3) / 16) * [о]
1000 Н * м ≤ ((π * d^3) / 16) * 60 МПа

Для упрощения расчета, давайте приведем значения к одним и тем же единицам измерения: Н * м и МПа.
1 Н * м = 1 Н * мм.
1 МПа = 1 Н / мм^2.

Подставляем значения:
1000 Н * м ≤ ((π * d^3) / 16) * 60 Н/мм2

Для удобства, давайте выразим диаметр вала, d:
1000 ≤ ((π * d^3) / 16) * 60

Для дальнейшего упрощения, давайте выразим π / 16 ≈ 0,2:
1000 ≤ 0,2 * d^3 * 60

Упростив, получаем:
1000 ≤ 12 * d^3

Разделив обе части неравенства на 12, получаем:
1000/12 ≤ d^3

Выполняя расчет, получаем:
≈ 83,3 ≤ d^3

Возведем обе части неравенства в 1/3 степень (корень третьей степени) для нахождения значения d:
(≈ 83,3)^(1/3) ≤ d

Используя калькулятор, получаем:
d ≤ 4,16

Получается, что диаметр вала должен быть меньше или равен 4,16 мм.

Итак, ответом на данный вопрос является:
Диаметр вала (по третьей теории прочности) не должен превышать 4,16 мм.

Помните, что это только один из возможных подходов к решению задачи, и в жизни может потребоваться дополнительные расчеты или учет других факторов.