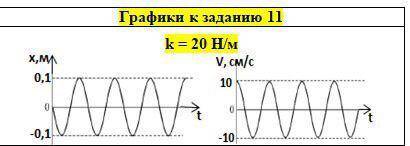
11. Груз, закреплённый на лёгкой пружине жёсткостью 200 Н/м, совершает вертикальные колебания. На рисунке изображены графики зависимости смещения x груза от времени t и проекции Vx скорости груза от времени. Определите, чему равна масса груза. ответ выразите в системе СИ

Для определения массы груза, мы можем воспользоваться следующим соотношением:

Т = 2π√(m/k),

где T - период колебаний, m - масса груза, k - жёсткость пружины.

Период колебаний можно определить по графику зависимости смещения x груза от времени t.

Смотря на график, можно заметить, что один полный период колебаний составляет 10 секунд. Таким образом, период колебаний груза равен T = 10 секунд.

Теперь мы можем использовать данное значение периода и соотношение T = 2π√(m/k) для определения массы груза.

Для начала, мы должны определить значение жёсткости пружины k. На графике проекции Vx скорости груза от времени, можно заметить, что амплитуда колебаний скорости составляет 4 м/с.

Таким образом, мы можем записать следующее соотношение:

A = 2π√(m/k),

где A - амплитуда колебаний скорости.

Подставив значение амплитуды, мы получаем:

4 = 2π√(m/k).

Решая это уравнение относительно жесткости k, мы можем найти:

k = (4/2π)² = 4/π² ≈ 1,27 Н/м².

Итак, мы теперь знаем значение жесткости пружины k и период колебаний T. Мы можем использовать соотношение T = 2π√(m/k), чтобы определить массу груза:

10 = 2π√(m/1,27).

Решая это уравнение, мы можем найти:

√(m/1,27) = 10/(2π),

m/1,27 = (10/(2π))²,

m ≈ 1,080 кг.

Таким образом, масса груза приближенно равна 1,080 кг.