1. Вычислить наибольшую и наименьшую длины волн К-серии характеристического рентгеновского излучения от платинового антикатода. 2. За какое время распадается 87,5% ядер атомов 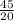Сa?

1. Чтобы вычислить наибольшую и наименьшую длину волн для К-серии характеристического рентгеновского излучения от платинового антикатода, нам понадобится знание энергии связи электрона в атоме платины.

В атоме платины, происходит эмиссия рентгеновского излучения при взаимодействии падающих электронов с электронами внутренних слоев. Наибольшая длина волны в районе K-серии соответствует переходу электрона из L-оболочки на K-оболочку, а наименьшая длина волны соответствует переходу с M-оболочки на K-оболочку.

Для вычисления энергии связи электрона в атоме платины можно использовать формулу Ридберга:

E = Rh * (Z - σ)^2 / n^2

где E - энергия связи электрона, Rh - константа Ридберга, Z - эффективный заряд ядра атома платины, σ - экранирующая константа, n - главное квантовое число электрона.

Для атома платины Z равно 78, и мы можем взять σ около 1, а для K-оболочки n равно 1, для L-оболочки n равно 2, а для М-оболочки n равно 3.

Теперь, чтобы вычислить энергию связи электрона, нам нужно вставить значения в формулу Ридберга:

E(K-оболочка) = Rh * (78 - 1)^2 / 1^2
E(L-оболочка) = Rh * (78 - 1)^2 / 2^2
E(M-оболочка) = Rh * (78 - 1)^2 / 3^2

2. Чтобы решить задачу о распаде 87,5% ядер атомов Ca за определенное время, нам понадобятся знания о периоде полураспада и законе радиоактивного распада.

Период полураспада (T) - это время, за которое количество радиоактивных ядер уменьшается в два раза. Закон радиоактивного распада гласит, что количество оставшихся ядер (N) в зависимости от времени (t) описывается формулой:

N = N0 * (1/2)^(t / T)

где N0 - начальное количество ядер, N - количество оставшихся ядер через время t, и T - период полураспада.

Для решения задачи мы знаем, что 87,5% ядер атомов Ca распалось, поэтому количество оставшихся ядер будет равно 12,5% от начального количества ядер (N0).

Используя формулу и известное количество оставшихся ядер, мы можем решить уравнение:

12,5% * N0 = N0 * (1/2)^(t / T)

Для решения этого уравнения мы можем использовать метод логарифмирования. Получив значение для t, мы сможем ответить на вопрос о времени распада.